映射是一种对应关系。
函数是一种映射,将变量间的关系形式化为数学描述。
令(y = f(x)),即(y)是(x)的函数,可以是(y = 2x + 1),也可以是(y = sin(x))。(x)的变化将引起(y)的变化,(x)的变化量(triangle x)导致(y)变化(triangle y),当变化量很小(趋近于0)时,为瞬间变化量,记为(dx)和(dy),瞬间变化量之比为瞬间变化率,即(frac{dy}{dx})。瞬间变化率(frac{dy}{dx})乘以(x)的瞬间变化量(dx)为(y)的瞬间变化量(dy)。
导数(Derivative),是对瞬间变化率的衡量,即(frac{dy}{dx}),导数也是函数,衡量每个(x)位置处的瞬间变化率。而微分(Differential,differentiation, differential calculus),指的是求导数——通过求瞬间变化量的关系来求导数。
当(x)为单变量时,导数为
[f'(a) = frac{dy}{dx} rvert _{x=a} = lim_{h rightarrow 0} frac{f(a + h) - f(a)}{h}]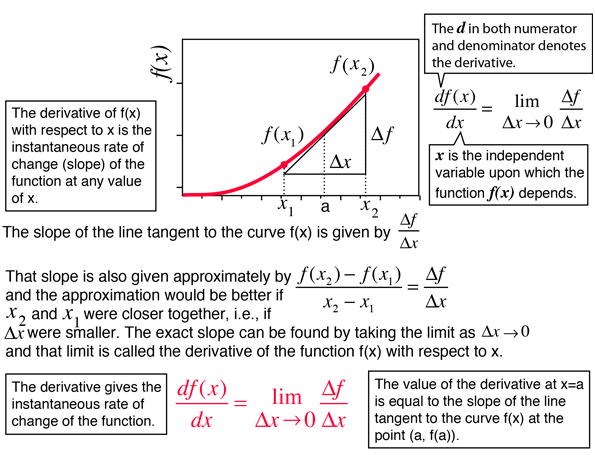
每个位置处的导数如下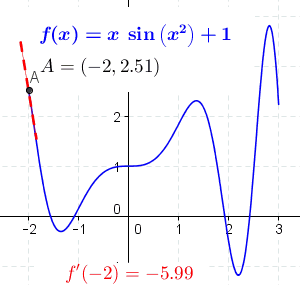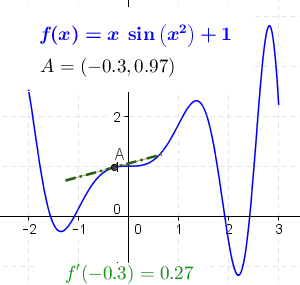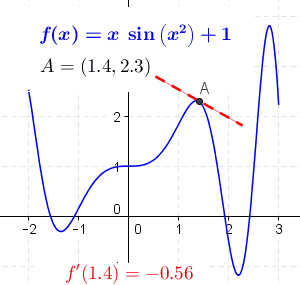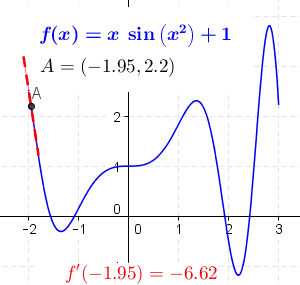
基本初等函数包括:幂函数、指数函数、对数函数、三角函数、反三角函数、常数函数。
基本初等函数通过四则运算和复合可以得到复杂函数,其中减法与加法等价,除法与乘法等价:
- 加法(减法):(f(x)+g(x))
- 乘法(除法):(f(x)g(x))
- 复合:(f(g(x)))
加法的求导可以理解为变化量(率)的叠加,即(f' + g');
乘法的求导可以理解为矩形面积的变化率,将(f(x))和(g(x))看成矩形的边长,导数为$(frac{(f + df)(g+dg)}{dx}),在(dx)趋近于0时,面积增量为(fdg+gdf)(忽略了极小项),即导数为(f'g+fg')。如下
复合函数的求导可以理解为变化率的传递,(y = f(u)),(u=g(x)),(x)的变化引起(u)的变化,(u)的变化引起(y)的变化,即(dy=frac{dy}{du} du =frac{dy}{du} frac{du}{dx} dx),(frac{dy}{dx}= frac{dy}{du} frac{du}{dx}),此为链式法则,(f'(x) = f'(g(x)) g'(x))。变化量的传递如下:
可以令(x)变化一个极小量如(triangle x=0.000001),带入函数求(y)的变化量(triangle y),用(frac{triangle y}{triangle x})来估计(x)位置的导数,但这无疑是费时费力的,常见函数的导数一般都存在解析形式,如下:
参考
- 还没有人评论,欢迎说说您的想法!




 客服
客服


