这个系列我们来聊聊序列标注中的中文实体识别问题,第一章让我们从当前比较通用的基准模型Bert+Bilstm+CRF说起,看看这个模型已经解决了哪些问题还有哪些问题待解决。以下模型实现和评估脚本,详见 Github-DSXiangLi/ChineseNER
NER问题抽象
实体识别需要从文本中抽取两类信息,不同类型的实体本身token组合的信息(实体长啥样),以及实体出现的上下文信息(实体在哪里)一种解法就是通过序列标注把以上问题转化成每个字符的分类问题,label主要有两种其中BIO更常见些
- BIO:B标记实体的开始,I标记其余部分,非实体是O
- BMOES:B标记开始,E标记结束,中间是M,单字实体是S,非实体是O
主流中文实体识别任务都是字符级输入,考虑后面会用到Bert-finetune统一用bert-tokenizer做字符到ID的映射。不以中文分词作为输入粒度的原因也很简单,其一分词本身的准确率限制了NER的天花板,其二不同领域NER的词粒度和分词的粒度会存在差异进一步影响模型表现。如何引入中文词粒度信息,之后会通过词汇增强的方式来实现。以下是训练数据的Demo

NER评估
NER评估分为Tag级别(B-LOC,I-LOC)和Entity级别(LOC),一般以entity的micro F1-score为准。因为tag预测准确率高但是抽取出的entity有误,例如边界错误,在实际应用时依旧抽取的是错误的实体。repo中的evalution.py会针对预测结果分别计算Tag和Entity的指标,以下是Bert-bilstm-crf在MSRA数据集上的表现
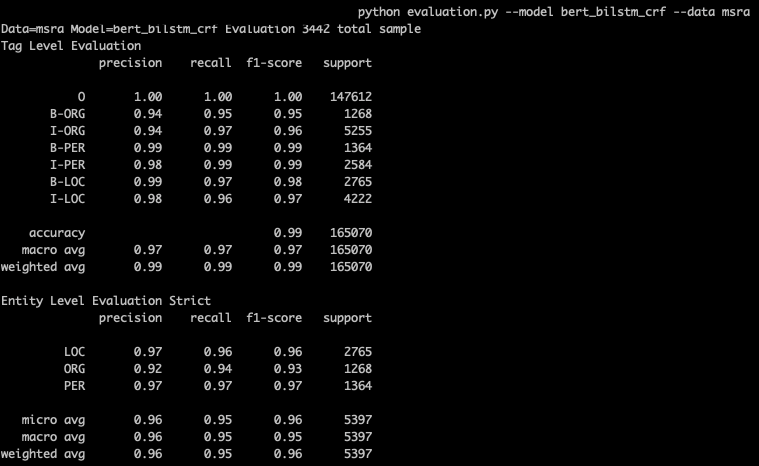
以上Entity级别的指标,针对预测抽取的实体和实际标注的实体进行计算
有两种聚合方式,micro是直接整体求precision,recall和F1。macro是分别计算各个实体类型的precision, recall和F1然后简单平均得到整体的结果。考虑到不同实体类型的占比往往存在差异(尤其是对细分类别的NER任务),所以整体评估一般以micro为准。在MSRA和people daily数据集上差别不大,因为只有3类实体且数据量差不太多。
基线模型 Bert-Bilstm-CRF
来看下基准模型的实现,输入是wordPiece tokenizer得到的tokenid,进入Bert预训练模型抽取丰富的文本特征得到batch_size * max_seq_len * emb_size的输出向量,输出向量过Bi-LSTM从中提取实体识别所需的特征,得到batch_size * max_seq_len * (2*hidden_size)的向量,最终进入CRF层进行解码,计算最优的标注序列。
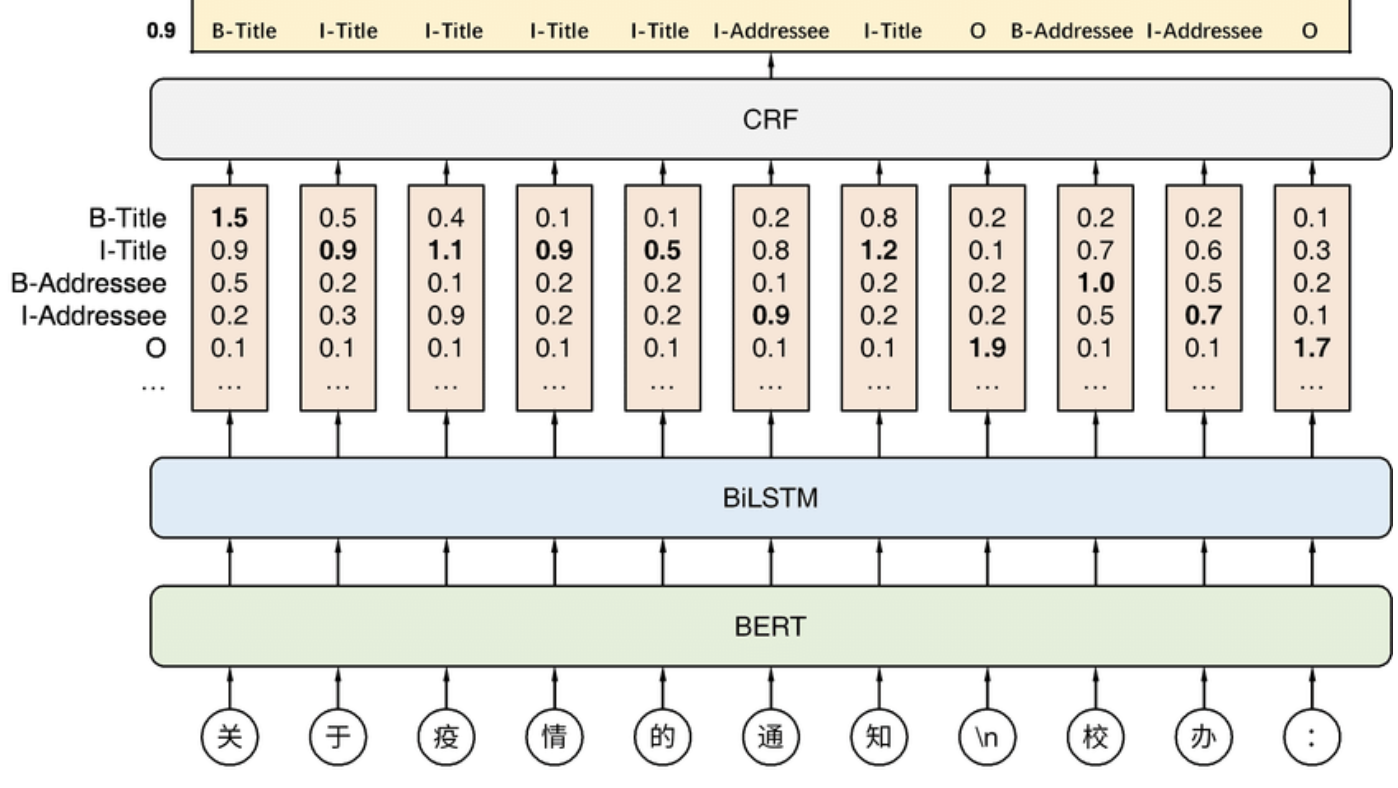
def build_graph(features, labels, params, is_training):
input_ids = features['token_ids']
label_ids = features['label_ids']
input_mask = features['mask']
segment_ids = features['segment_ids']
seq_len = features['seq_len']
embedding = pretrain_bert_embedding(input_ids, input_mask, segment_ids, params['pretrain_dir'],
params['embedding_dropout'], is_training)
load_bert_checkpoint(params['pretrain_dir']) # load pretrain bert weight from checkpoint
lstm_output = bilstm(embedding, params['cell_type'], params['rnn_activation'],
params['hidden_units_list'], params['keep_prob_list'],
params['cell_size'], params['dtype'], is_training)
logits = tf.layers.dense(lstm_output, units=params['label_size'], activation=None,
use_bias=True, name='logits')
add_layer_summary(logits.name, logits)
trans, log_likelihood = crf_layer(logits, label_ids, seq_len, params['label_size'], is_training)
pred_ids = crf_decode(logits, trans, seq_len, params['idx2tag'], is_training)
crf_loss = tf.reduce_mean(-log_likelihood)
return crf_loss, pred_ids
下面让我们从bottom到top,一层层来看Bert,bilstm和crf分别解决了哪些问题~
Layer1 - Bert:Contextual Embedding/Pretrain Language Model
解决问题:NER标注数据少,文本信息抽取效果不佳
paper:Semi-supervised sequence tagging with bidirectional language models
作者是18年提出ELMo的大神,他在16年就提出引入预训练语言模型可以提升序列标注效果。NER任务需要的文本信息可以大致分成词信息,考虑上下文的词信息,以及信息到实体类型的映射。paper指出预训练词向量(指Word2vec/glove这类静态不考虑上下文的词嵌入),只涵盖基于共现的独立词信息,而考虑上下文的词信息还是要用有限的NER标注数据来训练,往往会导致信息抽取效果不好,以及泛化效果不好。
于是作者在大规模无标注数据集上训练了双向LM,由BiLSTM的forward和bachward层拼接得到文本表征,用LM模型来帮助抽取更全面/通用的文本信息。在NER模型中第一层BiLSTM从NER标注数据中学习上下文信息,第二层BiLSTM的输入由第一层输出和LM模型的输出拼接得到,这样就可以结合小样本训练的文本表征和更加通用LM的文本表征。
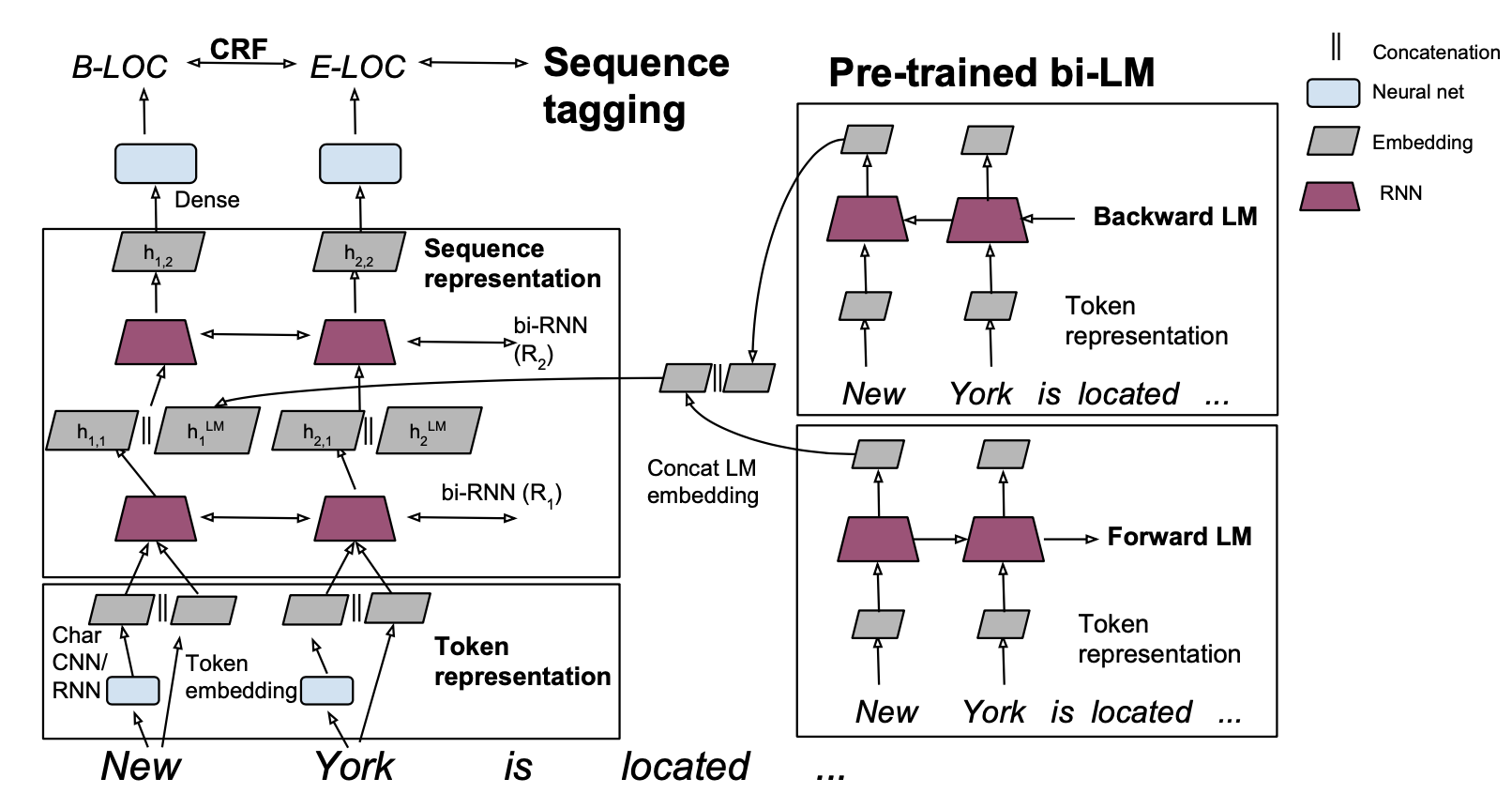
放在当下,预训练语言模型已经从Elmo一路到了各种bert,用法也和paper中略有区别。考虑到Bert强大的信息记忆和抽取能力,我们可以直接把Bert放在最底层用于抽取考虑上下文的文本信息。这里我对比了用bert的输入token embedding训练的bilstm-crf和finetune bert+bilstm-crf的效果。可以看到bert在entity级别的F1提升是惊人的,当然这个提升对于大样本的标注数据可能不会这么明显。
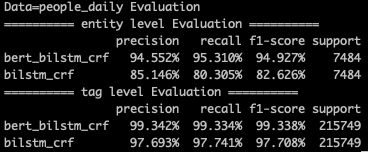
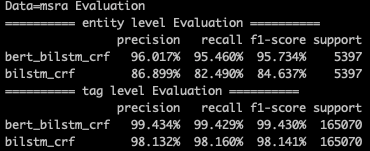
顺便说一下在实现的时候因为用了Bert所以要加入[SEP],[CLS]和[PAD],当时纠结了下这是都映射到1个label?还是各自映射到一个label?最后考虑到后面CRF转移矩阵的计算还是觉得各自映射到1个label会比较合适,看了下训练时打出的summary会发现step=100(其实应该在10以前)模型就已经完美的学到[SEP],[CLS],[PAD]了,所以对结果不会有任何影响滴

Layer2 - BiLSTM层真的需要么?
解决问题:抽取用于实体分类的包含上下文的文本信息
paper:Bidirectional LSTM-CRF Models for Sequence Tagging
16年的paper算是首篇把BiLSTM-CRF用于NER任务的尝试。Bilstm的存在是提取双向文本信息。和多数文本任务一样,如果想要speed up训练速度会考虑用CNN来替代RNN,想要捕捉kernel_size长度之外的信息,可以尝试stack-CNN或者拼接不同长度kernel_size的CNN。当时这些都是SOTA级别的模型,不过放在BERT出世后的今天,bilstm/cnn作为文本上下文信息提取的作用究竟还有多大嘞?
我简单比较了Bert-bilstm-crf,Bert-cnn-crf和Bert-crf在msra和people_daily数据集上的效果。在msra上确实有提升,不过在people daily上Bert-crf效果最好。整体上感觉bert把需要的信息都做了提取,bilstm只是选择性从中挑选有用的信息做整合,所以增益并不是很大。如果你的标注数据很少,或者对预测latency有要求,Bert-crf可能更合适些。
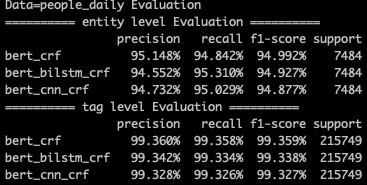
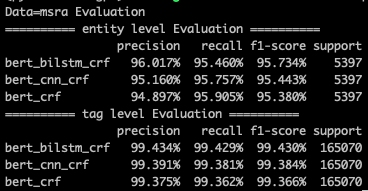
Layer3-Cross-entropy vs CRF
解决问题:实体内标签分类的一致性,T个N分类问题转化为(N^T)的分类问题
paper: Conditional Random Fields: Probabilistic Models for Segmenting and Labeling Sequence Data
把实体识别抽象为序列标注问题后,其中一个问题就是label的预测是独立的,但实体识别的准确率是把实体作为整体来计算的,所以需要考虑到实体内label预测的一致性,计算整个标注序列的全局最优,也就是把求解T个N分类问题转化为从(N^T)个序列中寻找概率最大的预测序列。序列标注模型经历了从HMM到MEMM再到CRF的更迭,让我们来简单对比下三个模型
1. HMM
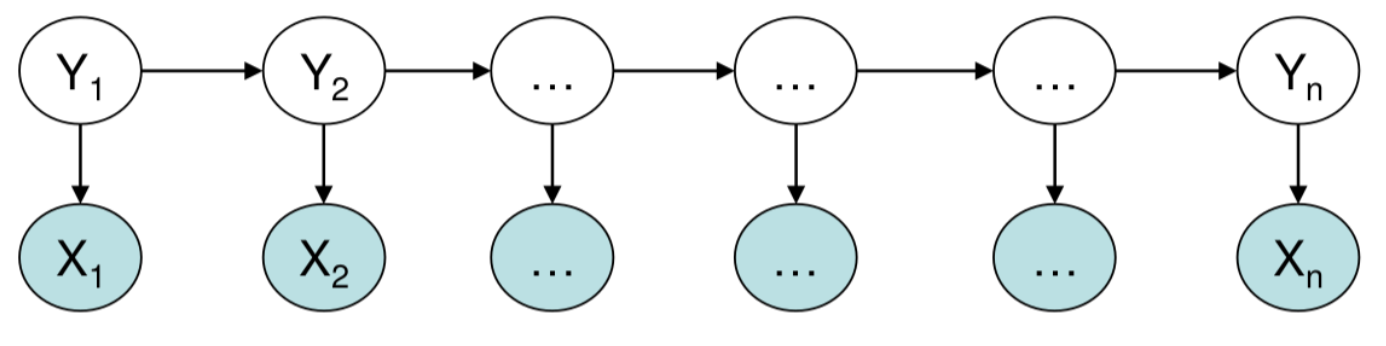
隐马尔可夫有向图模型,由观测序列和隐状态序列构成,在NER问题中观测序列就是输入句子,隐状态就是实体label,模型包含3个核心假设:
- 齐次马尔可夫性假设:(P(s_{t}|s_{1,2,...t-1})=P(s_{t}|s_{t-1})),当前实体label只和前一位置的label有关
- 不动性假设:转移概率矩阵和位置无关(P(s_i|s_{i-1})=P(s_j|s_{j-1}))
- 观测独立假设:观测只和当前位置隐状态有关(P(O_t|s_{1,2,...t-1},O_{1,2,...t-1})=P(O_t|s_t))
用HMM来对NER问题建模需要把条件概率先转化为联合概率如下
以上也就得到了HMM需要求解的三个变量
- 初始状态(P(s_0)):句子第一个label是B-PER/I-PER/.../O的概率
- 全局转移矩阵(P(s_t|s_{t-1})):B-PER->I-PER, I-PER->B-LOC,实体label间的转移概率
- 输出概率(P(O_t|s_t)):P(北|B-LOC)已知状态输出是某一token的概率
预测过程,既对已知观测序列,求解最有可能的状态序列。直接求解长度为T,label_size=N的序列是(O(N^T))的复杂度,通常采用动态规划的Viterbi算法来把复杂度降低到(O(N^2T)),详细的计算过程可以看文章最后的附录部分
看到这里你觉着用HMM来求解NER有啥问题嘞?主要问题有2个
- 观测独立假设,每个输出(character)当然不只依赖隐状态(label)还会依赖上下文信息
- HMM作为生成模型要计算联合概率,如果要引入额外特征来描述观测,例如大小写前缀后缀,需要计算每个特征的likelihood,所以很难引入额外特征。同时模型拟和的是联合概率,和预测需要的P(S|O)条件概率存在不一致。
2.MEMM
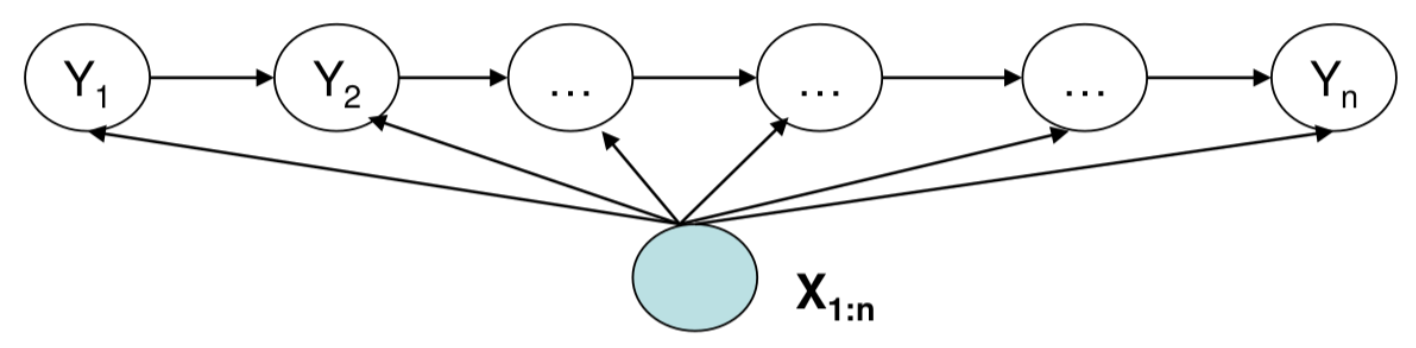
HMM在序列标注中的优势是隐状态间的跳转,会有效提高实体预测label之间的一致性。让我们保留优点,放松观测独立的假设,再把生成模型换成判别模型,直接对P(S|O)进行建模我们就得到了MEMM最大熵马尔可夫模型。MEMM可以方便的引入任意特征来对观测数据进行描述,并且没有观测独立假设后实体标签可以依赖任意上下文信息。
最大熵模型是对数线性模型,对滴就是熟悉的logistic regression,每个step都是多分类问题,输入F是基于t和t-1时刻的状态以及观测序列X构建的特征函数,输出是t时刻各个状态的概率(sum=1局部正则化),以下Z是正则因子
用MEMM求解给定观测下最优的标注序列如下
那用MEMM来求解NER还有啥问题勒?
- LabelBias: MEMM的局部正则化会导致预测时倾向于选择可转移状态更少的状态。很多博客都详细介绍了这个问题最大熵马尔可夫模型(MEMM)及其三个基本问题
3. CRF
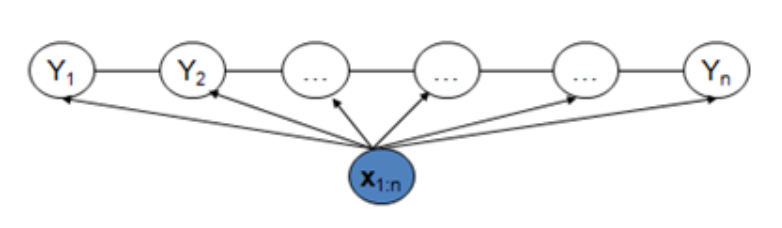
保留MEMM判别模型,马尔可夫状态转移,以及每个状态都依赖完整上下文的优点,CRF直接在全局进行正则化,解决了label bias的问题。对比MEMM在每个step进行正则化得到概率,CRF是直接对T个step所有(N^T)个可能状态路径计算全局概率进行正则化,如下
以上特征函数F可以进一步拆解成L个转移类特征和K个状态类特征之和
让我们来看下tensorflow中tf.contrib.crf的相关实现。其中转移特征函数是全局的转移矩阵,状态特征是最后一个layer输出的logit。解码同样是viterbi就不多说了,训练时loglikelihood的计算分为以下几步
- 计算真实序列的特征得分
- binary_score = (sum_{text{real path}} text{transition probabitliy})
- unary_score = (sum_{text{real path}} text{logits})
- sequence_score = bianry_score + unary_score
- 计算用于正则化的全部路径得分log_norm
crf_log_norm巧妙利用了矩阵计算把遍历所有路径(O(N^T))的复杂度降低到了(O(N^2T)), 每一步都是N*N的矩阵乘积运算在CrfForwardRnnCell中实现,细节可以去看李航大大的统计学习方法,简单来说就是定义矩阵M
- 输出crf_log_likelihood = sequence_score - log_norm
现在NER任务基本以加入CRF为主,让我们我们对比下在Bert输出层后直接加cross-entropy和CRF的效果差异如下。在tag级别cross-entropy和CRF基本是一样的,但因为加入了对Label转移概率的约束,CRF在entity级别的指标上有明显更高的召准。

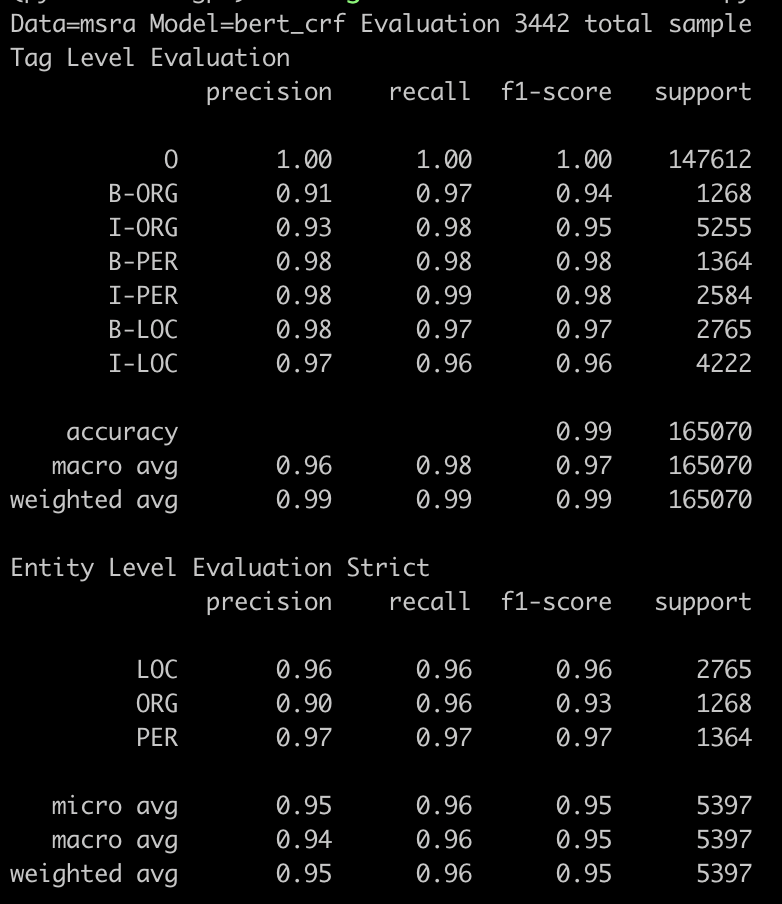
还要注意一点就是和Bert一起训练的CRF,最好使用不同的learning rate,Bert层是微调lr不能太高不然会出现信息遗忘,一般在(e^{-5}~e^{-6})。而这么小的lr会导致CRF层转移概率收敛太慢,CRF的lr一般需要乘100~500倍。更多细节可以看下【REF6】。代码实现采用了分层lr,按variable_scope来区分lr,越靠近输出层的lr越高。
基准模型在两个数据集上看起来好像已经很不错,但是在实际应用中还有许多需要解决的问题。例如NER标注样本太少如何解决,垂直领域迁移问题,中文词边界问题和词汇信息增强,Label Imbalance问题等等,我们在后面的章节再慢慢唠
Ref-A
- Conditional Random Fields: Probabilistic Models for Segmenting and Labeling Sequence Data, 2001
- Bidirectional LSTM-CRF Models for Sequence Tagging, 2015
- Named Entity Recognition with Bidirectional LSTM-CNNs, 2016
- Neural Architectures for Named Entity Recognition, 2016
- Semi-supervised sequence tagging with bidirectional language model
- 你的CRF层的学习率可能不够大
- http://www.davidsbatista.net/blog/2018/05/09/Named_Entity_Evaluation/
- https://zhuanlan.zhihu.com/p/103779616
Ref-B Viterbi
-
定义t时刻到达状态i的最大概率路径
[delta_t(i)=max_{s_1,..s_{t-1}}P(s_1,..,s_{t-1},s_t=i,O_1,...,O_t|pi,A,B) ] -
综合转移概率和输出概率,(delta_t(i))存在以下递归关系,因此每一步只需要做N->N个状态复杂度为(O(N^2))的递归计算
- 向前递归计算的同时记录每一步状态i前一刻的状态j,当递归到序列尽头,得到T时刻最大概率的状态再往前回溯,得到最大概率对应的状态序列
文章来源: 博客园
- 还没有人评论,欢迎说说您的想法!




 客服
客服


