关于“Unsupervised Deep Embedding for Clustering Analysis”的优化问题
作者:凯鲁嘎吉 - 博客园 http://www.cnblogs.com/kailugaji/
Deep Embedding Clustering (DEC)和Improved Ceep Emdedding Clustering (IDEC)被相继提出,但关于参数的优化问题,作者并未详细给出,于是乎自己推导了一遍,但是发现和这两篇文章的推导结果不一致,不知道问题出在哪?下面,相当于给出一道数学题,来求解目标函数关于某个参数(以聚类中心为例)的偏导问题。
问题描述
已知
[L=sumlimits_{i}^{N}{sumlimits_{j}^{c}{{{p}_{ij}}log frac{{{p}_{ij}}}{{{q}_{ij}}}}}]
[{{q}_{ij}}=frac{{{(1+{{left| {{z}_{i}}-{{mu }_{j}} right|}^{2}})}^{-1}}}{sumnolimits_{j}{{{(1+{{left| {{z}_{i}}-{{mu }_{j}} right|}^{2}})}^{-1}}}}]
[{{p}_{ij}}=frac{q_{ij}^{2}/sumnolimits_{j}{{{q}_{ij}}}}{sumnolimits_{j}{(q_{ij}^{2}/sumnolimits_{j}{{{q}_{ij}}})}}]
固定${p}_{ij}$, 求
[frac{partial L}{partial {{mu }_{j}}}]
问题求解
根据链式法则
[frac{partial L}{partial {{mu }_{j}}}=frac{partial L}{partial {{q}_{ij}}}frac{partial {{q}_{ij}}}{partial {{mu }_{j}}}]
[frac{partial L}{partial {{q}_{ij}}}=frac{partial left( {{p}_{ij}}log frac{{{p}_{ij}}}{{{q}_{ij}}} right)}{partial {{q}_{ij}}}=frac{partial left( {{p}_{ij}}log {{p}_{ij}}-{{p}_{ij}}log {{q}_{ij}} right)}{partial {{q}_{ij}}}=-frac{{{p}_{ij}}}{{{q}_{ij}}}]
[frac{{partial {q_{ij}}}}{{partial {mu _j}}} = sumlimits_i^N {frac{{partial frac{{{{(1 + {{left| {{z_i} - {mu _j}} right|}^2})}^{ - 1}}}}{{sumnolimits_j {{{(1 + {{left| {{z_i} - {mu _j}} right|}^2})}^{ - 1}}} }}}}{{partial {mu _j}}}} = sumlimits_i^N {left( {frac{{partial {{(1 + {{left| {{z_i} - {mu _j}} right|}^2})}^{ - 1}}}}{{partial {mu _j}}}frac{1}{{sumnolimits_j {{{(1 + {{left| {{z_i} - {mu _j}} right|}^2})}^{ - 1}}} }} + {{(1 + {{left| {{z_i} - {mu _j}} right|}^2})}^{ - 1}}frac{{partial frac{1}{{sumnolimits_j {{{(1 + {{left| {{z_i} - {mu _j}} right|}^2})}^{ - 1}}} }}}}{{partial {mu _j}}}} right)} ]
其中
[frac{{partial {{(1 + {{left| {{z_i} - {mu _j}} right|}^2})}^{ - 1}}}}{{partial {mu _j}}} = - {(1 + {left| {{z_i} - {mu _j}} right|^2})^{ - 2}} cdot left( { - 2({z_i} - {mu _j})} right) = 2({z_i} - {mu _j}) cdot {(1 + {left| {{z_i} - {mu _j}} right|^2})^{ - 2}}]
[frac{{partial frac{1}{{sumnolimits_j {{{(1 + {{left| {{z_i} - {mu _j}} right|}^2})}^{ - 1}}} }}}}{{partial {mu _j}}} = - frac{{2({z_i} - {mu _j}) cdot {{(1 + {{left| {{z_i} - {mu _j}} right|}^2})}^{ - 2}}}}{{{{left( {sumnolimits_j {{{(1 + {{left| {{z_i} - {mu _j}} right|}^2})}^{ - 1}}} } right)}^2}}}]
所以
[frac{{partial {q_{ij}}}}{{partial {mu _j}}} = sumlimits_i^N {(frac{{2 cdot ({z_i} - {mu _j}) cdot {{(1 + {{left| {{z_i} - {mu _j}} right|}^2})}^{ - 2}}}}{{sumnolimits_j {{{(1 + {{left| {{z_i} - {mu _j}} right|}^2})}^{ - 1}}} }} - frac{{2 cdot ({z_i} - {mu _j}) cdot {{(1 + {{left| {{z_i} - {mu _j}} right|}^2})}^{ - 2}} cdot {{(1 + {{left| {{z_i} - {mu _j}} right|}^2})}^{ - 1}}}}{{{{left( {sumnolimits_j {{{(1 + {{left| {{z_i} - {mu _j}} right|}^2})}^{ - 1}}} } right)}^2}}})} = sumlimits_i^N {left( {2 cdot ({z_i} - {mu _j}) cdot {{(1 + {{left| {{z_i} - {mu _j}} right|}^2})}^{ - 1}} cdot {q_{ij}} - 2 cdot ({z_i} - {mu _j}) cdot {{(1 + {{left| {{z_i} - {mu _j}} right|}^2})}^{ - 1}} cdot q_{ij}^2} right)} {rm{ = }}sumlimits_i^N {left( {2 cdot ({z_i} - {mu _j}) cdot {{(1 + {{left| {{z_i} - {mu _j}} right|}^2})}^{ - 1}} cdot {q_{ij}} cdot (1 - {q_{ij}})} right)} ]
求导结果
[frac{{partial L}}{{partial {mu _j}}} = frac{{partial L}}{{partial {q_{ij}}}}frac{{partial {q_{ij}}}}{{partial {mu _j}}} = sumlimits_i^N {left( { - frac{{{p_{ij}}}}{{{q_{ij}}}} cdot 2 cdot ({z_i} - {mu _j}) cdot {{(1 + {{left| {{z_i} - {mu _j}} right|}^2})}^{ - 1}} cdot {q_{ij}} cdot (1 - {q_{ij}})} right)} = sumlimits_i^N {left( {2 cdot ({z_i} - {mu _j}) cdot {{(1 + {{left| {{z_i} - {mu _j}} right|}^2})}^{ - 1}} cdot {p_{ij}} cdot ({q_{ij}} - 1)} right)} ]
原文结果
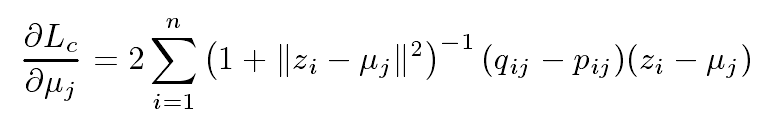
不知道问题出在哪?求广大网友指正~
参考文献
[1] Deep Clustering Algorithms - 凯鲁嘎吉 博客园
[2] Xie J, Girshick R, Farhadi A. Unsupervised deep embedding for clustering analysis[C]//International conference on machine learning. 2016: 478-487.
[3] Guo X, Gao L, Liu X, et al. Improved deep embedded clustering with local structure preservation[C]//IJCAI. 2017: 1753-1759.
文章来源: 博客园
- 还没有人评论,欢迎说说您的想法!




 客服
客服


