树链剖分详解

542 0 0

作者:Heartquakes

前言
一、树剖是什么？
二、重链剖分
树剖的实现
例题
总结

前言

在同学们一路走来的过程中，一定已经学习了倍增求 LCA 的算法。

倍增求 LCA 算法只适用于少部分情况，那么，如果要求在求出 LCA 的同时，对两点 (a, b) 之间的所有点权（或边权）进行求和或修改，又该怎么做呢？这里介绍一种 树链剖分 的方法（树链剖分有多种，这里只介绍其中用途最广的一种，重链剖分）。

随笔同步发布于 CSDN。

一、树剖是什么？

顾名思义，树链剖分就是将整棵树剖分为若干条链，使它组合成一个线性结构，然后用其他的数据结构维护树上的信息。

重链剖分 可以将树上的任意一条路径划分成不超过 (O(log n)) 条连续的链，保证划分出的每条链上的节点 DFS 序 连续，因此可以方便地使用 线段树 之类的数据结构来维护树上的信息。

二、重链剖分

首先，我们要明确一些定义：

重子节点：某个点的子节点中子树最大的子结点。如果有多个子树最大的子结点，取其中任意一个即可。如果该点没有子节点，就无重子节点。
轻子节点：除重子节点以外的所有子结点。
重边：从节点到重子节点的边。
轻边：从节点到轻子节点的边。
重链：由若干条首尾衔接的重边构成的链。

若我们把无重子节点的点也当成一条重链，则这棵树就可以被划分成若干条互不相交的重链。容易发现，一颗子树内的 DFS 序是连续的。这也方便了我们维护字树内的值。

其实有一种树剖方试叫轻链剖分，划分的方法与重链剖分类似，这里不多赘述。

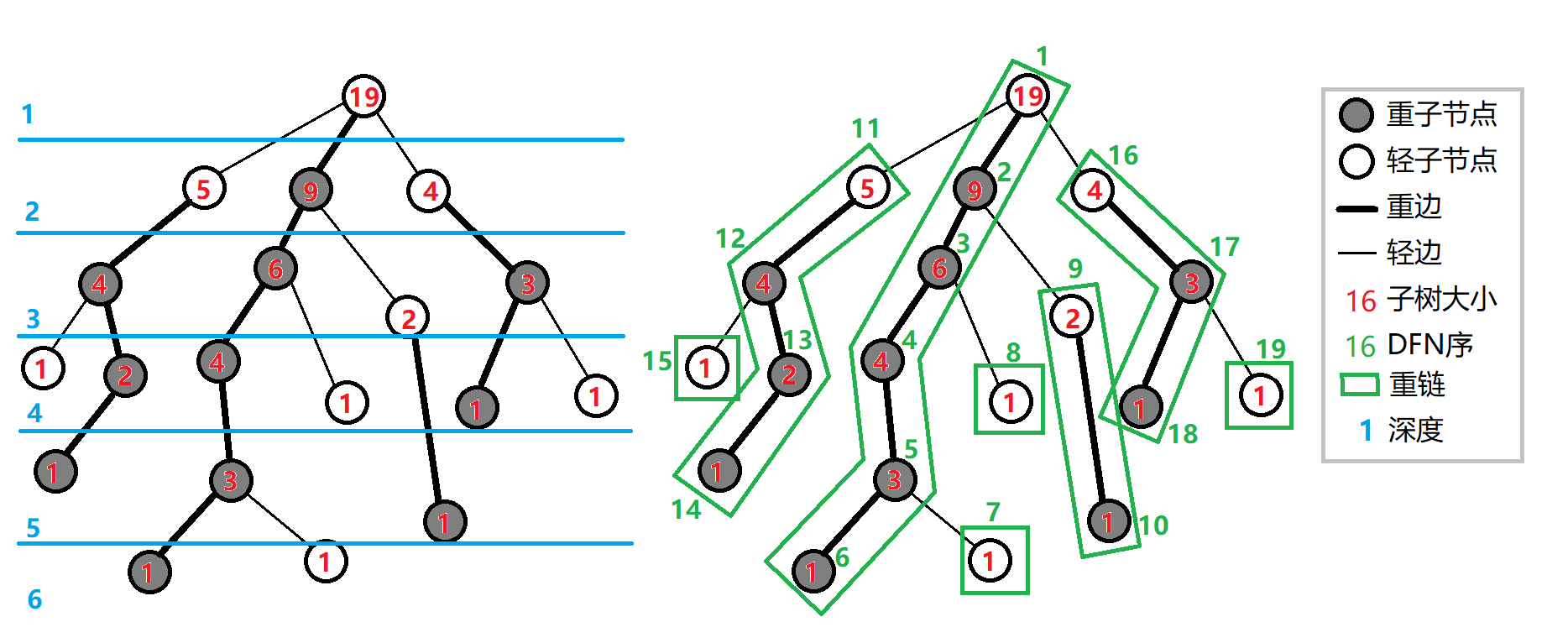注：图片引自 OI-WIKI。

树剖的实现

重剖的实现是由两个 DFS 完成的。

对于每个节点 (u)：

用第一个 DFS 记录每个结点的父节点（记作 (f_u)）、深度（记作 (dep_u)）、子树大小（记作 (son_u)）、重子节点（记作 (heavy_u)）。
第二个 DFS 则记录所在链的头（记作 (top_u)）、按先重边后轻边的顺序遍历时的 DFS 序（记作 (dfn_u)）、DFS 序对应的节点编号（由于 C++ 中 (texttt{rank}) 为关键字，记作 (ranki_u)）。显然，有 (ranki_{dfn_u}=u)。

修改部分：

对于每次两点之间路径上的点的区间修改或查询操作，将两个点沿着重链不断向上跳祖先，由于每条链内的点的 DFS 序一定是连续的，所以区间修改/查询 (dfn_{top_x} sim dfn_x) 即可。
对于以某个顶点为根的子树的修改操作，由于这棵子树内的 DFS 序连续（上文已说明），区间修改/查询 (dfn_x sim dfn_x+son_x-1) 即可。
使用 线段树 维护修改标记即可。

模板题代码（洛谷 P3384 【模板】重链剖分/树链剖分）：

// Problem: P3384 【模板】重链剖分/树链剖分
// Contest: Luogu
// URL: https://www.luogu.com.cn/problem/P3384
// Memory Limit: 128 MB
// Time Limit: 1000 ms
// 
// Powered by CP Editor (https://cpeditor.org)

#include <bits/stdc++.h>
using namespace std;

#define int long long
const int N = 100005;

int n, m, r, p, tot, opt, x, y, z, cnt;
int heavy[N], son[N], dfn[N], top[N], ranki[N], val[N], dep[N], f[N], head[N];

struct edge
{
	int to, nxt;
}e[N << 1];

struct node
{
	int l, r, tag, sum;
}tree[N << 2];

inline void add_edge(int x, int y)
{
	e[++tot] = {y, head[x]}, head[x] = tot;
}

inline void dfs1(int u, int fa)
{
	dep[u] = dep[fa] + 1, f[u] = fa, son[u] = 1;
	for(int i = head[u]; ~i; i = e[i].nxt)
	{
		int v = e[i].to;
		if(v == fa) continue;
		dfs1(v, u);
		son[u] += son[v];
		if(son[v] > son[heavy[u]]) heavy[u] = v;
	}
	return;
}

inline void dfs2(int u, int tp)
{
	top[u] = tp, dfn[u] = ++cnt, ranki[dfn[u]] = u;
	if(!heavy[u]) return;
	dfs2(heavy[u], tp);
	for(int i = head[u]; ~i; i = e[i].nxt)
	{
		int v = e[i].to;
		if(v != f[u] && v != heavy[u]) dfs2(v, v);
	}
	return;
}

inline void push_up(int x)
{
	tree[x].sum = tree[x << 1].sum + tree[x << 1 | 1].sum;
}

inline void push_down(int x)
{
	tree[x << 1].tag += tree[x].tag, tree[x << 1].tag %= p;
	tree[x << 1 | 1].tag += tree[x].tag, tree[x << 1 | 1].tag %= p;
	tree[x << 1].sum = (tree[x << 1].sum + tree[x].tag * (tree[x << 1].r - tree[x << 1].l + 1)) % p;
	tree[x << 1 | 1].sum = (tree[x << 1 | 1].sum + tree[x].tag * (tree[x << 1 | 1].r - tree[x << 1 | 1].l + 1)) % p;
	tree[x].tag = 0;
}

inline void build(int l, int r, int x)
{
	tree[x] = {l, r, 0, 0};
	if(l == r) return (void) (tree[x].sum = val[ranki[l]] % p);
	int mid = l + r >> 1;
	build(l, mid, x << 1);
	build(mid + 1, r, x << 1 | 1);
	push_up(x);
}

inline void update(int l, int r, int k, int x)
{
	if(l <= tree[x].l && tree[x].r <= r)
		return (void) (tree[x].tag = (tree[x].tag + k) % p, tree[x].sum = (tree[x].sum + k * (tree[x].r - tree[x].l + 1)) % p);
	int mid = tree[x].l + tree[x].r >> 1;
	push_down(x);
	if(l <= mid) update(l, r, k, x << 1);
	if(r > mid) update(l, r, k, x << 1 | 1);
	push_up(x);
}

inline int query(int l, int r, int x)
{
	if(l <= tree[x].l && tree[x].r <= r) return tree[x].sum;
	int mid = tree[x].l + tree[x].r >> 1, ans = 0;
	push_down(x);
	if(l <= mid) ans += query(l, r, x << 1);
	if(r > mid) ans += query(l, r, x << 1 | 1);
	push_up(x);
	return ans % p;
}

inline void change(int x, int y, int z)
{
	while(top[x] != top[y])
	{
		if(dep[top[x]] < dep[top[y]]) swap(x, y);
		update(dfn[top[x]], dfn[x], z, 1);
		x = f[top[x]];
	}
	if(dfn[x] > dfn[y]) swap(x, y);
	update(dfn[x], dfn[y], z, 1);
}

inline int ask(int x, int y)
{
	int ans = 0;
	while(top[x] != top[y])
	{
		if(dep[top[x]] < dep[top[y]]) swap(x, y);
		ans = (ans + query(dfn[top[x]], dfn[x], 1)) % p;
		x = f[top[x]];
	}
	if(dfn[x] > dfn[y]) swap(x, y);
	return (ans + query(dfn[x], dfn[y], 1)) % p;
}

signed main()
{
	ios :: sync_with_stdio(false);
	memset(head, -1, sizeof head);
	cin >> n >> m >> r >> p;
	for(int i = 1; i <= n; i++) cin >> val[i];
	for(int i = 1; i < n; i++)
	{
		cin >> x >> y;
		add_edge(x, y);
		add_edge(y, x);
	}
	dfs1(r, 0);
	dfs2(r, 0);
	build(1, n, 1);
	while(m--)
	{
		cin >> opt;
		if(opt == 1)
		{
			cin >> x >> y >> z;
			change(x, y, z);
		}
		else if(opt == 2)
		{
			cin >> x >> y;
			cout << ask(x, y) % p << 'n';
		}
		else if(opt == 3)
		{
			cin >> x >> z;
			update(dfn[x], dfn[x] + son[x] - 1, z, 1);
		}
		else if(opt == 4)
		{
			cin >> x;
			cout << query(dfn[x], dfn[x] + son[x] - 1, 1) % p << 'n';
		}
	}
	return 0;
}