二进制是计算技术中广泛采用的一种数制。二进制数据是用0和1两个数码来表示的数。利用二进制的特点,可以用于枚举一个集合中各元素的所有组合情况。
例如,设某集合M中有3个元素A、B和C,即M={A,B,C}。可以用3位二进制数来枚举3个元素的各种组合情况(也可以称为子集),每一位二进制数字对应一个元素,1表示选中,0表示不选。
二进制数 001,表示选中A元素,B和C元素不选择,即子集为 { A };
二进制数 010,表示选中B元素,A和C元素不选择,即子集为 { B };
二进制数 011,表示选中A和B元素,C元素不选择,即子集为 { A,B };
二进制数 100,表示选中C元素,A和B元素不选择,即子集为 { C };
二进制数 101,表示选中A和C元素,B元素不选择,即子集为 { A,C };
二进制数 110,表示选中B和C元素,A元素不选择,即子集为 { B,C };
二进制数 111,表示选中A、B和C这3个元素均选中,即子集为 { A,B,C };
当然,二进制数000表示3个元素均不选择,就是子集是空集。
这样,用循环 for (int i = 0; i < (1 << n); i++) 就可以遍历每一个子集,即遍历各种组合情况。其中 (1 << n)表示 2n ,2n-1就对应n为二进制数,各位上的数字均为1。
然后,可以利用二进制的位运算,来判断二进制数的某一位上是0还是1。
二进制位运算的左移运算 a << b就表示把a转为二进制后左移b位(即在后面添b个0)。
这样, 1<<0=1(0) ; 1<<1=2 (10); 1<<2=4 (100); 1<<3=8 (1000);
……
因此,要判断一个二进制数x的第k位上是0还是1,只需计算 x & (1<<K),若计算出来的值为0,则x的第k位为0;若计算出来的值非0,则x的第k位为0。
这样,再利用循环
For (int j = 0; j < n; j++)
if (i & (1 << j)) { … }
就可以对每一个子集中所选取的具体元素进行处理。
编写如下的示例程序。
#include <stdio.h> int main() { char s[6]="ABCDE"; int n; scanf("%d",&n); int i,j; for (i=0; i<(1<<n); i++) // 枚举从0~2^n-1中组合情况 { printf("[ "); for (j = 0; j < n; j++) // 遍历二进制的每一位 { if (i & (1 << j)) // 判断二进制第j位是否为1,若为1,表示元素选中 { printf("%c ",s[j]); // 如果第j个元素选中,则输出 } } printf("]n"); } return 0; }
该程序运行后,输入3,可以输出A、B、C这3个元素的8中组合情况。运行结果如下所示。
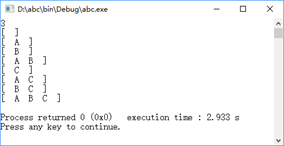
下面通过一些实例来看二进制枚举的应用方法。
【例1】最接近的和
问题描述
给出两个整数n(n≤20)和b,然后给出n个整数h1、h2、…、hn。问如何在这n个整数里面选择若干个数使得它们的和在满足大于等于b的情况下最小,并输出这个和与b的差。
输入
第1行:2个用空格隔开的整数:N和B。
第2…N+1行:第i+1行是1个整数:Hi。
输出
输出1个非负整数,即满足大于等于b的情况下的最小和值与b的差。
输入样例
5 16
3
1
3
5
6
输出样例
1
(1)编程思路。
直接套用上面的二进制枚举的模板对h1、h2、…、hn这n个元素的各种组合情况进行处理。只是在具体处理时,将每次挑选中的元素累加起来。当和值大于等于b时,记录最小的和值即可。
(2)源程序。
#include <stdio.h> int main() { int n,b; scanf("%d%d",&n,&b); int i,j,h[21]; for (i=0;i<n;i++) scanf("%d",&h[i]); int ans=0x3f3f3f3f; for (i=0; i<(1<<n); i++) // 枚举从0~2^n-1中组合情况 { int sum=0; for (j = 0; j < n; j++) // 遍历二进制的每一位 { if (i & (1 << j)) // 判断二进制第j位是否为1,若为1,表示元素选中 { sum+=h[j]; // 如果第j个元素选中,则加上它 } } if (sum>=b) { if (sum<ans) ans=sum; } } printf("%dn",ans-b); return 0; }
将上面的源程序提交给 洛谷题库 P2677 [USACO07DEC]Bookshelf 2 B(https://www.luogu.com.cn/problem/P2677),可以Accepted。
【例2】权利指数
问题描述
在选举问题中,总共有n个小团体,每个小团体拥有一定数量的选票数。如果其中m个小团体的票数和超过总票数的一半,则此组合为“获胜联盟”。n个团体可形成若干个获胜联盟。一个小团体要成为一个“关键加入者”的条件是:在其所在的获胜联盟中,如果缺少了这个小团体的加入,则此联盟不能成为获胜联盟。一个小团体的权利指数是指:一个小团体在所有获胜联盟中成为“关键加入者”的次数。请你计算每个小团体的权利指数。
输入
输入数据的第一行为一个正整数T,表示有T组测试数据。每一组测试数据的第一行为一个正整数n(0<n<=20)。第二行有n个正整数,分别表示1到n号小团体的票数。
输出
对每组测试数据,在同一个行按顺序输出1到n号小团体的权利指数。
输入样例
2
1
10
7
5 7 4 8 6 7 5
输出样例
1
16 22 16 24 20 22 16
(1)编程思路。
同样直接套用上面的二进制枚举的模板对n个小团体的各种组合情况进行处理。若某个团体组合的得票数超过了总票数的一半,则依次对该组合中的每个小团队进行判断,若去掉了某个小团体后,得票数小于总票数的一半,则去掉的小团体就是关键加入者,进行计数。
(2)源程序。
#include <stdio.h> #include <string.h> int main() { int t; scanf("%d", &t); while (t--) { int a[21],key[21], ans[21]; memset(ans, 0, sizeof(ans)); int n,total = 0; scanf("%d", &n); int i; for (i = 0; i < n; i++) { scanf("%d", &a[i]); total += a[i]; } total /= 2; for (i = 1; i < 1 << n; i++) // 二进制枚举各团体组合 { int j, k = 0, sum = 0; for (j = 0; j < n; j++) // 遍历二进制的每一位 { if (i & (1 << j)) // 判断二进制第j位是否为1 { key[k++] = j; sum += a[j]; } } if (sum > total) // 如果团体的票数超过总票数的一半 { for (j = 0; j < k; j++) if (sum - a[key[j]] <= total) // 编号为key[j]的元素为 关键加入者 ans[key[j]]++; } } printf("%d", ans[0]); for (i = 1; i < n; i++) printf(" %d", ans[i]); printf("n"); } return 0; }
将上面的源程序提交给 HDU题库 HDU 1557 权利指数(http://acm.hdu.edu.cn/showproblem.php?pid=1557),可以Accepted。
【例3】目标和习惯
问题描述
小明有很多习惯,比如看电影、听音乐、玩电脑游戏和足球等等。此外,他还有很多目标,因为不是每个习惯都有助于实现他的目标,他陷入了在目标和习惯之间做出选择的困境。
现在,我们将一个习惯对每个目标的影响定义为向量,向量的元素是整数,例如。向量(100,90,-10,80)表示它对目标1有100分的影响,对目标2有90分的影响、对目标3有-10分的影响和对目标4有80分的影响(正表示良好效果,负表示不良效果),每个目标的给定要求表示为整数。请帮助小明实现他的目标,并尽可能多地保持他的习惯。
输入
有多种情况,读取数据直到EOF。(不超过10例)
第1行:小明的目标数N(0<N<=20)
第2行:每个目标的要求(0<w<=1000)
第3行:小明的习惯数M(0<M<=16)
第4-M+4行:每行包含N个整数,第i个整数表示对第i个目标的影响(-1000<=data<=1000)。
输出
对于每种情况:输出是一行,其中包含:
小明可以保持的最大习惯数,其次是:
小明可以保持的习惯的排序列表(从最小到最大)。如果有一组以上的习惯可以满足要求,请选择习惯数最少的一组。
如果无法实现小明的目标,请输出0。
输入样例
4
100 200 300 400
3
100 100 400 500
100 -10 50 300
100 100 -50 -50
输出样例
2 1 3
(1)编程思路。
采用二进制枚举对m个习惯的全部组合情况进行处理。对每种习惯组合,将组合中的各习惯对目标的影响累加到数组g中。若数组g中每个目标均可实现,则是一种满足要求的习惯组合。
(2)源程序。
#include <stdio.h> #include <string.h> int main() { int goal[21]; int f[17][21],g[21]; int n; while (scanf("%d",&n)!=EOF) { int ans1=-1,ans2; int i,j,k; for (i=0;i<n;i++) scanf("%d",&goal[i]); int m; scanf("%d",&m); for (i=0;i<m;i++) for(j=0;j<n;j++) scanf("%d",&f[i][j]); for (i=0;i<(1<<m);i++) // 对所有m个习惯的组合进行枚举 { for (k=0;k<n;k++) g[k]=0; // 各目标的达到值初始化为0 int num=0; // 当前组合中的习惯个数 for (j=0;j<m;j++) if (i&(1<<j)) // 若组合中有第j个习惯 { num++; for (k=0;k<n;k++) // 第j个习惯对每个目标k的影响 g[k]+=f[j][k]; } for (k=0;k<n;k++) if (g[k]<goal[k]) break; // 第k个目标不能实现 if (k==n) // 当前习惯组合中,所有目标可达成 { if (num>ans1) { ans1=num; ans2=i; } } } if (ans1==-1) printf("0n"); else { printf("%d",ans1); for (i=0;i<n;i++) if (ans2&(1<<i)) printf(" %d",i+1); printf("n"); } } return 0; }
将上面的源程序提交给 HDU题库 HDU 4152 ZZY’s Dilemma(http://acm.hdu.edu.cn/showproblem.php?pid=4152),可以Accepted。
【例4】调查问卷
问题描述
度度熊为了完成毕业论文,需要收集一些数据来支撑他的论据,于是设计了一份包含 m 个问题的调查问卷,每个问题只有 'A' 和 'B' 两种选项。
将问卷散发出去之后,度度熊收到了 n 份互不相同的问卷,在整理结果的时候,他发现可以只保留其中的一部分问题,使得这 n 份问卷仍然是互不相同的。这里认为两张问卷是不同的,当且仅当存在至少一个被保留的问题在这两份问卷中的回答不同。
现在度度熊想知道,存在多少个问题集合,使得这 n 份问卷在只保留这个集合的问题之后至少有 k 对问卷是不同的。
输入
第一行包含一个整数 T,表示有 T 组测试数据。
接下来依次描述 T 组测试数据。对于每组测试数据:
第一行包含三个整数 n,m 和 k,含义同题目描述。
接下来 n 行,每行包含一个长度为 m 的只包含 'A' 和 'B' 的字符串,表示这份问卷对每个问题的回答。
保证 1≤T≤100,1≤n≤103,1≤m≤10,1≤k≤106,给定的 n 份问卷互不相同。
输出
对于每组测试数据,输出一行信息 "Case #x: y"(不含引号),其中 x 表示这是第 x 组测试数据,y 表示满足条件的问题集合的个数,行末不要有多余空格。
输入样例
2
2 2 1
AA
BB
2 2 2
AA
BB
输出样例
Case #1: 3
Case #2: 0
(1)编程思路。
先把每张问卷对10个问题回答的A、B字符串转换成二进制数保存在数组a中,转换时,A转换为1,B转换为0。
采用二进制枚举的方法依次枚举每个可能的子集(选择部分问题的情况,下面将枚举到的某个二进制数i称为当前状态),与每张问卷的这个子集情况(当前状态i)下的答案匹配。具体做法是:将当前状态i与每张试卷的答案(也已转换为了二进制数并保存在数据元素a[j]中)进行与运算,即now=i & a[j],并将cnt[now]加1。显然,若问卷j和问卷k的答案相同,则a[j]与a[k]的值一定相同,这样now的值也相同,cnt[now]的值会加上2。
当匹配到第j张问卷时,第j张问卷与前面的j-1张问卷在当前选择状态i下一定有cnt[i&a[j]]张(包括第j张)的答案相同,也就是有j- cnt[i&a[j]]张的答案存在不同,将它累加到和值sum上。当某个当前状态i与每张问卷匹配完成后,如果和值sum大于或等于k,这种当前状态 i 就是符合题意的一种子集选择。遍历所有可能的子集,就得到最终的答案。
(2)源程序。
#include <stdio.h> #include <string.h> int main() { int t,iCase=0; scanf("%d",&t); while (t--) { int n, m, k; scanf("%d%d%d",&n,&m,&k); int a[1001]; int i,j; for (i=1; i<=n; i++) { char s[15]; scanf("%s",s); int num=0; for (j=0; s[j]!='�'; j++) // 第i张问卷对10个问题回答的A、B字符串转换成二进制数保存在数组a[i] { if (s[j]=='A') num=num*2+1; else num=num*2; } a[i] = num; } int ans = 0; for (i=1; i<(1<<m); i++) // 对m个问题的全部组合情况进行枚举 { int cnt[1050]; memset(cnt, 0, sizeof(cnt)); int sum = 0; for (j=1; j<=n; j++) { int now = i & a[j]; cnt[now]++; sum += j-cnt[now]; } if(sum>=k) ans++; } printf("Case #%d: %dn",++iCase,ans); } return 0; }
将上面的源程序提交给 HDU题库 HDU 6344 调查问卷(http://acm.hdu.edu.cn/showproblem.php?pid=6344),可以Accepted。
【例5】连续求余
问题描述
有一个整数a和n个整数b1,…,bn。在按任意顺序从b1、…、bn中选择一些数字后,例如c1、…、cr,我们希望确保a mod c1 mod c2 mod…mod cr=0(即,a将成为每次除以ci的余数,最后,我们希望a变为0)。请确定r的最小值。如果无法实现目标,请输出−1代替。
输入
第一行包含一个整数T≤5,表示测试用例的数量。
对于每个测试用例,有两行:
第一行包含两个整数n和a(1≤n≤20,1≤a≤106)。
第二行包含n个整数b1,…,bn(1≤bi≤106)
输出
每个测试用例输出1行,该行中输出所求得的最小的r值。
输入样例
2
2 9
2 7
2 9
6 7
输出样例
2
-1
(1)编程思路。
采用二进制枚举的方法对b1、…、bn中的数的各种选择组合进行处理。只是在本题处理时,需要先将数组b按从大到小的顺序进行排列。因为,若先选择一个小的数进行求余,则后面较大的数的选择毫无意义。
(2)源程序。
#include <stdio.h> int main() { int t; scanf("%d",&t); while (t--) { int n,a,b[25]={0}; scanf("%d%d",&n,&a); int i,j; for (i=0;i<n;i++) scanf("%d",&b[i]); for (i=0;i<n-1;i++) // 将数组b按从大到小的顺序排列 for (j=0;j<n-1-i;j++) if (b[j]<b[j+1]) { int temp; temp=b[j]; b[j]=b[j+1]; b[j+1]=temp; } int ans=25; // 所以数全部选,不会超过20个数 for (i=0;i<(1<<n);++i) { int res=a,cnt=0; for (j=0;j<n;++j) { if(i>>j&1) { res=res%b[j]; cnt++; if(res==0)break; } } if (res==0) ans=(cnt<ans)?cnt:ans; } if(ans==25) printf("-1n"); else printf("%dn",ans); } return 0; }
将上面的源程序提交给 HDU题库 HDU 5339 Untitled(http://acm.hdu.edu.cn/showproblem.php?pid=5339),可以Accepted。
在通过上面的5道例题的学习,掌握了二进制枚举方法的应用的基础上,可以刷一下HDU题库中的下面几道题目,也均可采用二进制枚举的方法来完成。
【练习1】HDU 1882 Strange Billboard (http://acm.hdu.edu.cn/showproblem.php?pid=1882)。

#include <stdio.h> #include <string.h> int main() { int r,c; while (scanf("%d%d",&r,&c)!=EOF) { if (r==0 && c==0) break; int i,j,k; char map[20][20],temp[20][20]; for (i=0;i<r;++i) scanf("%s",map[i]); if (r<c) // 若行数小于列数,则使矩阵转置。 { memcpy(temp,map,sizeof(map)); for (i=0;i<r;++i) { for (j=0;j<c;++j) { map[j][i]=temp[i][j]; } } k=r; r=c; c=k; } int hash[20],key[20]; for(i=0;i<r;++i) // 将第i行数据以二进制形式保存在数组元素hash[i]中,‘X’符号位置1 { hash[i]=0; for (j=0;j<c;++j) { if (map[i][j]=='X') hash[i]=(hash[i]<<1)^1; else hash[i]=(hash[i]<<1); } } int ans=1000; // 按题意,最多256个方格,因此翻转次数肯定不会超过1000 for (i=0; i<(1<<c); i++) // 对第0行的所有翻转组合进行二进制枚举 { int cnt=0; memcpy(key,hash,sizeof(hash)); // 将初始画面情况数组hash暂存到key数组中 for (j=0;j<c;j++) // 处理第0行(首行) { if (i & (1<<(c-1-j))) { key[0]^=(1<<(c-1-j)); // 当前方块翻转 if (j-1>=0) // 当前方块左边(前一列)的方块翻转 key[0]^=(1<<(c-1-j+1)); if (j+1<c) // 当前方块右边(后一列)的方块翻转 key[0]^=(1<<(c-1-j-1)); if (1<r) // 当前方块下方(下一行)的方块翻转 key[1]^=(1<<(c-1-j)); cnt++; // 翻转次数加1 } } for (j=1;j<r;++j) // 上1行确定了,下一行只能根据上一行进行处理。依次处理后面的r-1行 { for (k=0;k<c;++k) // 对当前行的每列的方块进行判断,根据正上方的方块状态看是否需要翻转 { if (key[j-1]&(1<<(c-1-k))) // 当前方块正上方方块为'X‘,需要翻转当前方块 { cnt++; key[j]^=(1<<(c-1-k)); // 当前方块翻转 if (k-1>=0) // 当前方块左边(前一列)的方块翻转 key[j]^=(1<<(c-1-k+1)); if (k+1<c) // 当前方块右边(后一列)的方块翻转 key[j]^=(1<<(c-1-k-1)); if (j-1>=0) // 当前方块上方(上一行)的方块翻转 key[j-1]^=(1<<(c-1-k)); if (j+1<r) // 当前方块下方(下一行)的方块翻转 key[j+1]^=(1<<(c-1-k)); } } } if (!key[r-1]) // 由于下一行必受上一行约束,则只要判断最后行是否达到要求即可 { if (ans>cnt) ans=cnt; } } if (ans<1000) printf("You have to tap %ld tiles.n",ans); else printf("Damaged billboard.n"); } return 0; }
【练习2】HDU 3118 Arbiter (http://acm.hdu.edu.cn/showproblem.php?pid=3118)。

#include <stdio.h> int main() { int t; scanf("%d",&t); while (t--) { int n,m; scanf("%d%d",&n,&m); int map[305][2]; int i,j; for (i=0;i<m;i++) { scanf("%d%d",&map[i][0],&map[i][1]); } int ans=0x3f3f3f3f; for (i=0;i<(1<<n);i++) { int cnt=0; for (j=0;j<m;j++) { if (((i>>map[j][0]) & 1)==((i>>map[j][1])&1)) cnt++; } if (cnt<ans) ans=cnt; } printf("%dn",ans); } return 0; }
【练习3】 HDU 4462 Scaring the Birds (http://acm.hdu.edu.cn/showproblem.php?pid=4462) 。

#include <stdio.h> #include <string.h> int abs(int x) { return x>0?x:-x; } int main() { int n; while (scanf("%d", &n) && n!=0) { int m; scanf("%d", &m); int i,j; int r[51],c[51],f[51]; for (i = 0; i < m; i++) scanf("%d%d", &r[i], &c[i]); for (i = 0; i < m; i++) scanf("%d", &f[i]); int ans = 100; for (i = 0; i < (1 << m); i++) // 二进制枚举各位置放置稻草人的组合情况 { int num = 0; // 放稻草人的个数 int a[10],vis[51][51]; memset(vis, 0, sizeof(vis)); for (j = 0; j < m; j++) if (i&(1 << j)) a[num++] = j; // 保存所放稻草人的编号 int flag = 1; int x,y,z; for (x = 1; x <= n; x++) // 放置了num个稻草人后,看稻田所有位置是否全部覆盖 { for (y = 1; y <= n; y++) { for (z = 0; z < m; z++) if (r[z] == x && c[z] == y) vis[x][y] = 1; if (vis[x][y]) continue; for (z = 0; z < num; z++) { if (abs(x - r[a[z]]) + abs(y - c[a[z]]) <= f[a[z]]) { vis[x][y] = 1; break; } } if (vis[x][y] == 0) // 当前位置(x,y)不能覆盖 flag = 0; if (!flag) break; } if (!flag) break; } if (flag) if (ans>num) ans=num; } if (ans == 100) printf("-1n"); else printf("%dn", ans); } return 0; }
【练习4】HDU 5616 Jam's balance(http://acm.hdu.edu.cn/showproblem.php?pid=5616)。

#include <stdio.h> #include <string.h> int main() { int t; scanf("%d",&t); while (t--) { int vis[2005]; memset(vis,0,sizeof(vis)); int n; scanf("%d",&n); int i,j,a[21]; for (i=0; i<n; i++) scanf("%d",&a[i]); for (i=0; i<(1<<n); i++) // 二进制有n位,枚举二进制数 { int sum=0; // 当前砝码组合可称出的总重量 for (j=0; j<n; j++) { if (i&(1<<j)) sum+=a[j]; } vis[sum]=1; for (j=0; j<n; j++) // 将每个砝码放在天平另一边 { if (sum-a[j]>=0) vis[sum-a[j]]=1; } } int m,x; scanf("%d",&m); while (m--) { scanf("%d",&x); if (vis[x]) printf("YESn"); else printf("NOn"); } } return 0; }
【练习5】HDU 6435 Problem J. CSGO (http://acm.hdu.edu.cn/showproblem.php?pid=6435)。

#include <stdio.h> int main() { int t; scanf("%d",&t); while (t--) { int n,m,K; scanf("%d%d%d",&n,&m,&K); long long mw[35],sw[35]; // K最大为5,2^5=32。性能组合情况不超过32种 int i,j,k; for (i=0;i<32;i++) mw[i] = sw[i] = -1e16; // 为求最大值,主、副武器的每种性能组合情况均预置一个很小的数 int s,x[6]; long long ret; for (i=0;i<n;i++) // 依次处理每个主武器 { scanf("%d",&s); for (j=0;j<K;j++) scanf("%d",&x[j]); for (j=0;j<(1<<K);j++) // 对当前主武器的性能组合进行二进制枚举 { ret = s; for (k=0;k<K;k++) ret += x[k]*((1&(j>>k))?1:-1); if (mw[j]<ret) mw[j]=ret; } } for (i=0;i<m;i++) // 依次处理每个副武器 { scanf("%d",&s); for (j=0;j<K;j++) scanf("%d",&x[j]); for (j=0;j<(1<<K);j++) // 对当前副武器的性能组合进行二进制枚举 { ret = s; for (k=0;k<K;k++) ret += x[k]*((1&(j>>k))?1:-1); if (sw[j]<ret) sw[j]=ret; } } long long ans = 0; for (i=0;i<(1<<K);i++) { ret=mw[i]+sw[(1<<K)-1-i]; // 主、副武器二进制位要求互补 if (ans<ret) ans=ret; } printf("%lldn",ans); } return 0; }
文章来源: 博客园
- 还没有人评论,欢迎说说您的想法!





 客服
客服


