1
如何判断一个数是否为奇数?
//常规方法
bool isOdd_Method1(int n)
{
if (n % 2)
return true;
else
return false;
}
//高效方法
bool isOdd_Method2(int n)
{
//奇数的二进制形式最后一位一定是1
return n & 0x1;
}
注:二进制除了最后一位其他均是2的倍数,故如为奇数,则二进制形式的最后一位一定为1.
2
如何判断一个整数是否为2的幂?
bool isPowerof2_Method1(unsigned n)
{
unsigned i = 1;
//i = 1,2,4,8,...
while (i < n)
{
i <<= 1;
}
//i >= n
return i == n;
}
bool isPowerof2_Method2(unsigned n)
{
//2的整数幂的二进制形式,只有一位为1,其余均为0
//此方法n不可以取0
return (n * n - 1) == 0;
}
示例: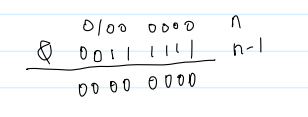
3
给定一个不为0的整数,找出last set bit.
例:
输入 0011 0100
输出 4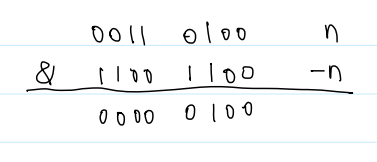
int lastSetBit(int n)
{
return n & -n;
}
4
给定一个数组,里面的整数都是成对出现的,只有一个数例外,请找出这个数。
例:
输入:[1,2,3,4,4,5,2,3,1]
输出:5
关键要知道异或运算的性质:
- a ^ 0 = a
- a ^ a = 0
- a ^ b = b ^ a
- (a ^ b) ^ c = a ^ (b ^ c)
int findSigleNum(int arr[], int n)
{
int sigleNum = 0;
for (int i = 0; i < n; i++)
{
sigleNum ^= arr[i];
}
return sigleNum;
}
4_拓展
给定一个数组,里面的整数都是成对出现的,只有两个数例外,请找出这两个数。
例:
输入:[1,2,3,4,4,5,2,3,1,6]
输出:5 6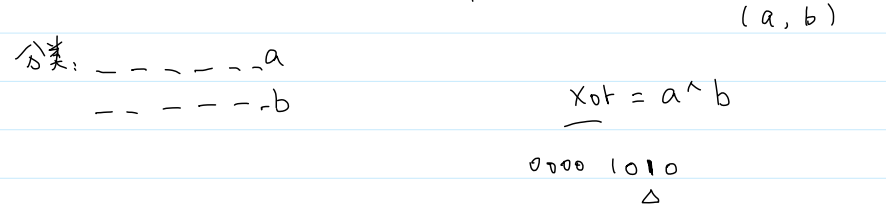
void findSigleNum(int arr[], int n, int* pa, int* pb)
{
int tmp = 0;
for (int i = 0; i < n; i++)
{
tmp ^= arr[i];
}
// 此时tmp = a ^ b,即要找的两个数的异或
/*tmp有个特点,即它的二进制形式从右向左为1(异或运算,不同为1)的一位就是这两个不同的数第一个不相同的一位
故根据此特征将整组数分为两组数,再分别在这两组数里找到例外的这个数即是最终结果*/
int lastSetBit = tmp & (-tmp);
for (int i = 0; i < n; i++)
{
if (arr[i] & lastSetBit)
{
*pa ^= arr[i];
}
else
{
*pb ^= arr[i];
}
}
}
内容来源于网络如有侵权请私信删除
文章来源: 博客园
- 还没有人评论,欢迎说说您的想法!




 客服
客服


