「观前提醒」
「文章仅供学习和参考,如有问题请在评论区提出」
一些扫描线问题的整理。
引入
扫描线一般被用来解决一些图形问题,像图形面积、周长,以及二维数点问题等。
Atlantis 问题(矩形面积问题)
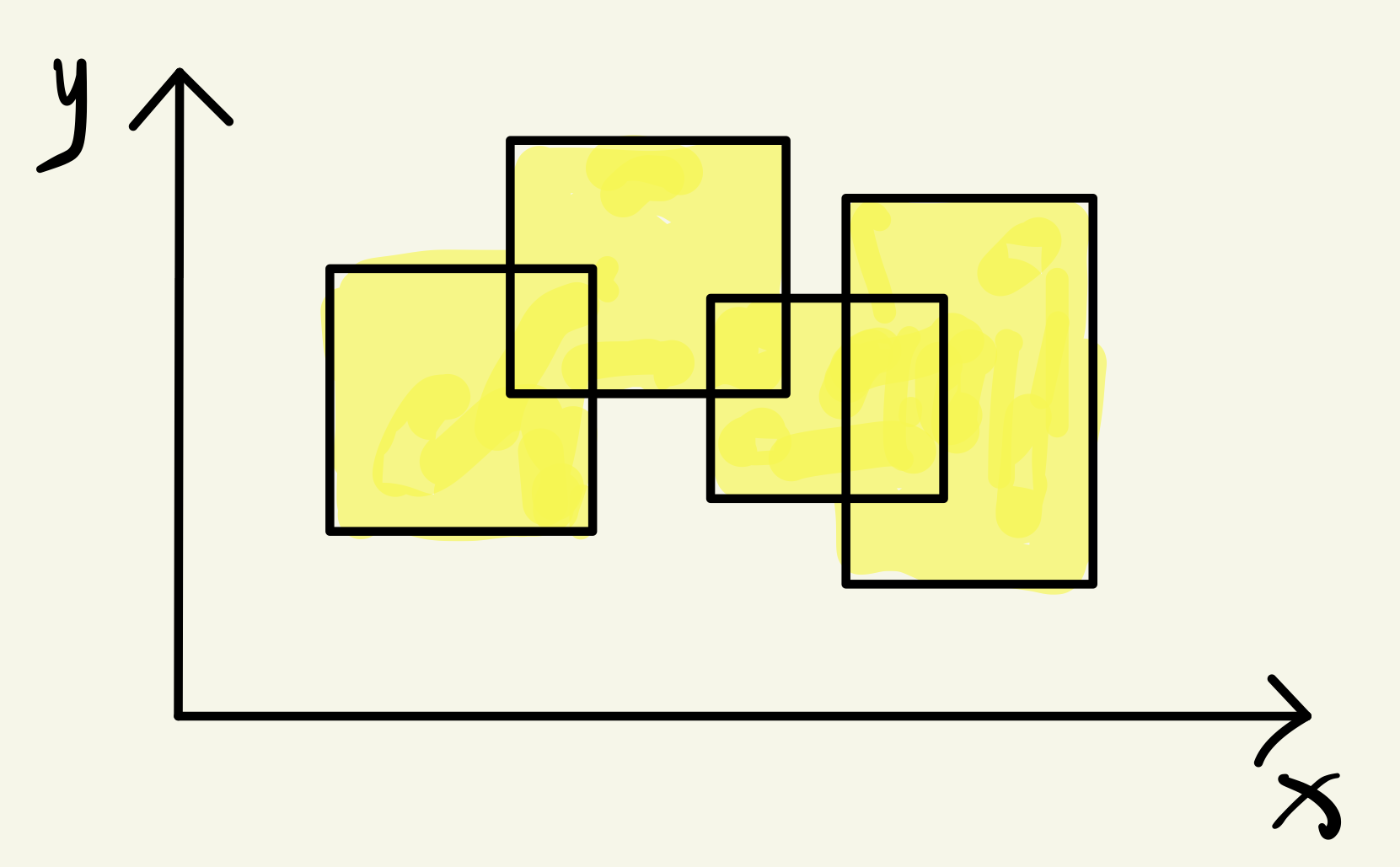
在二维坐标系上,给出多个矩形的左下和右上坐标 ((x1, y1), (x2, y2)) ,求出所有矩形构成的图形的面积。
观察上面的图形,我们可以通过扫描线来把它分成不同的小矩形,如下图所示
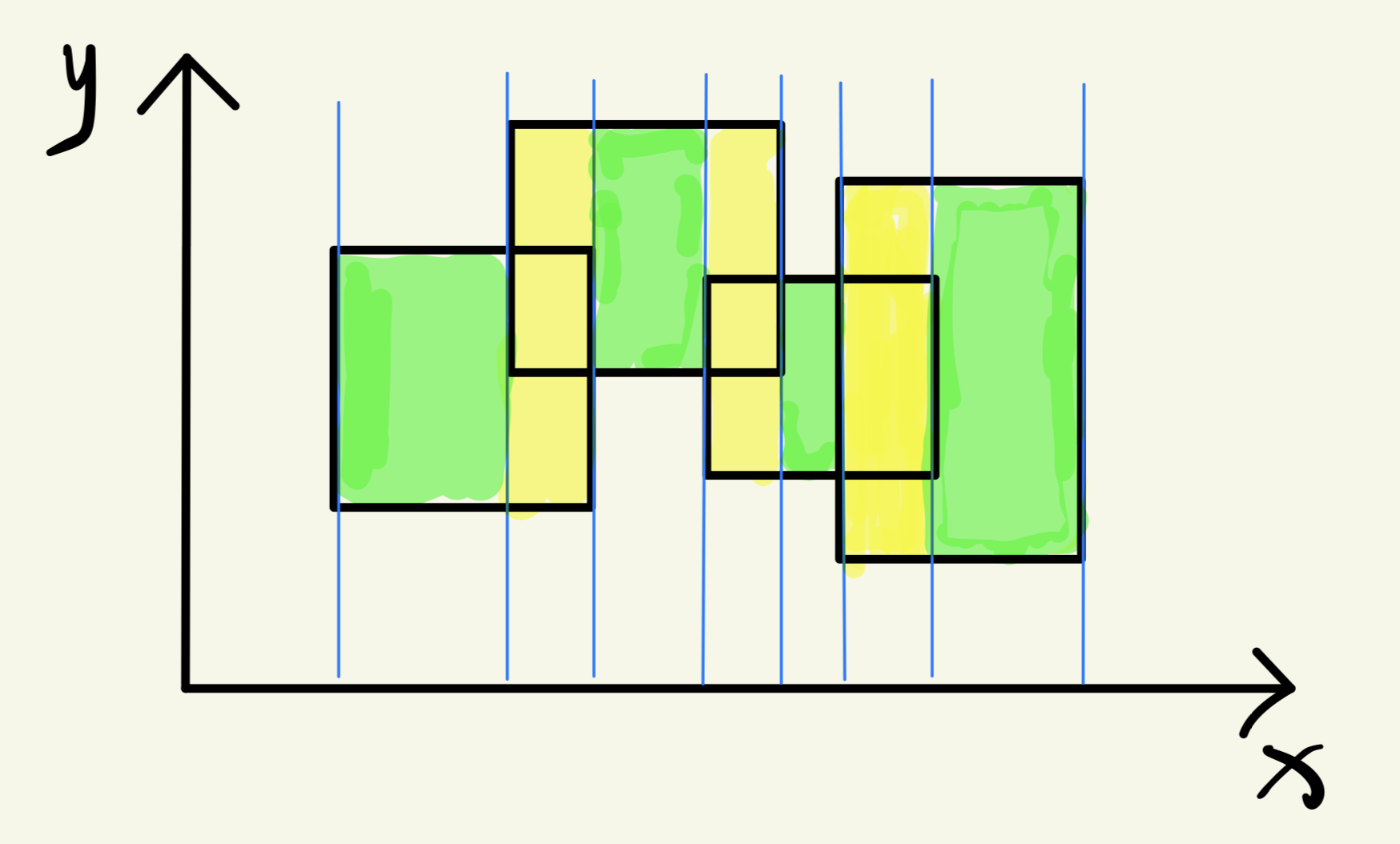
那么这样的话我们就可以从小到大枚举每一个 (x) 坐标,那么就能得到每一个小矩形的长度,然后再乘以每个矩形的高度就可以了。而每个小矩阵高度的维护就需要用到线段树。
我们要先给原先的每个矩形的左右边进行标记,矩形左边界标记为 (1) ,矩形右边界标记为 (-1) 。
那么我们之后在从左到右扫描的时候,对于标记为 (1) 的边,我们就加进来一条矩形的高,对于标记为 (-1) 的边,我们就删去这一条矩形的高。总体就是一个不断增删高度值的过程,增删一个矩阵对于此时高度的贡献值。
线段树所维护的是一个 (y) 坐标的区间值,而且对于坐标数据很大的情况下,需要离散化后再进行操作。
这样枚举每一个 (x) 坐标对有效高度更新,线段树每次更新是 (O(logN)) ,所以总的求解时间复杂度为 (O(NlogN)) 。
P5490 【模板】扫描线 - 洛谷
求 (n) 个四边平行于坐标轴的矩形的面积并。
#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
const int N = 2e5 + 10;
struct Tree { // 线段树
int l, r; // 所维护的区间
int len; // 区间的有效高度
int cnt; // 区间被覆盖的次数
} tr[N * 8]; // 开8倍防止越界
struct Line { // 扫描线
int x, y1, y2; // 每个 x 边界所对应的矩形的 下边界 y1, 上边界 y2
int op; // 左边界 1, 右边界 1
bool operator<(const Line &w) { // 重载, 用来排序
return x < w.x;
}
} X[N * 2];
int Y[N * 2]; // 所有 y 坐标
int n;
// 建树
void build(int u, int l, int r) {
tr[u] = {Y[l], Y[r]}; // 区间赋值
if (l + 1 == r) return; // 子区间, 返回
int mid = l + r >> 1;
build(u << 1, l, mid), build(u << 1 | 1, mid, r);
}
// 更新节点的区间有效高度
void pushup(int u) {
if (tr[u].cnt) // 此节点的区间依旧处于覆盖状态,
tr[u].len = tr[u].r - tr[u].l; // 区间有效高度就是区间宽度
else // 此区间并不处于完全覆盖状态
// 区间有效高度取决于左右节点的区间有效高度
tr[u].len = tr[u << 1].len + tr[u << 1 | 1].len;
}
// 更新操作
void update(int u, int l, int r, int op) {
if (tr[u].r <= l || tr[u].l >= r) return; // 越界区间, 返回
if (tr[u].l >= l && tr[u].r <= r) { // 区间被完全包含
tr[u].cnt += op; // 更新覆盖次数
pushup(u); // 更新实际区间长度
return;
}
// 向下拆分
update(u << 1, l, r, op), update(u << 1 | 1, l, r, op);
// 回溯更新
pushup(u);
}
int main() {
cin >> n;
for (int i = 1; i <= n; i++) {
int x1, y1, x2, y2;
scanf("%d%d%d%d", &x1, &y1, &x2, &y2);
X[i] = {x1, y1, y2, 1}; // 左边界, op = 1
X[n + i] = {x2, y1, y2, -1};// 右边界, op = -1
Y[i] = y1, Y[n + i] = y2; // 存储所有的 y 坐标
}
n *= 2;
// 排序
sort(X + 1, X + n + 1);
sort(Y + 1, Y + n + 1);
build(1, 1, n); // 建树
LL res = 0;
for (int i = 1; i < n; i++) {
// 每次更新高度, 每次更新完的新高度就是根节点的区间有效高度
update(1, X[i].y1, X[i].y2, X[i].op);
// 计算小矩形的面积: 宽 * 高
res += (LL)(X[i + 1].x - X[i].x) * tr[1].len;
}
cout << res << endl;
return 0;
}
二维数点
给一个长度为 (n) 的序列,有 (m) 次查询,每次查询区间 ([l, r]) 中值在 ([x, y]) 内的元素个数。
这种问题可以等价为求一个二维平面上矩形内的点的个数,而主要做法就是扫描线+树状数组。
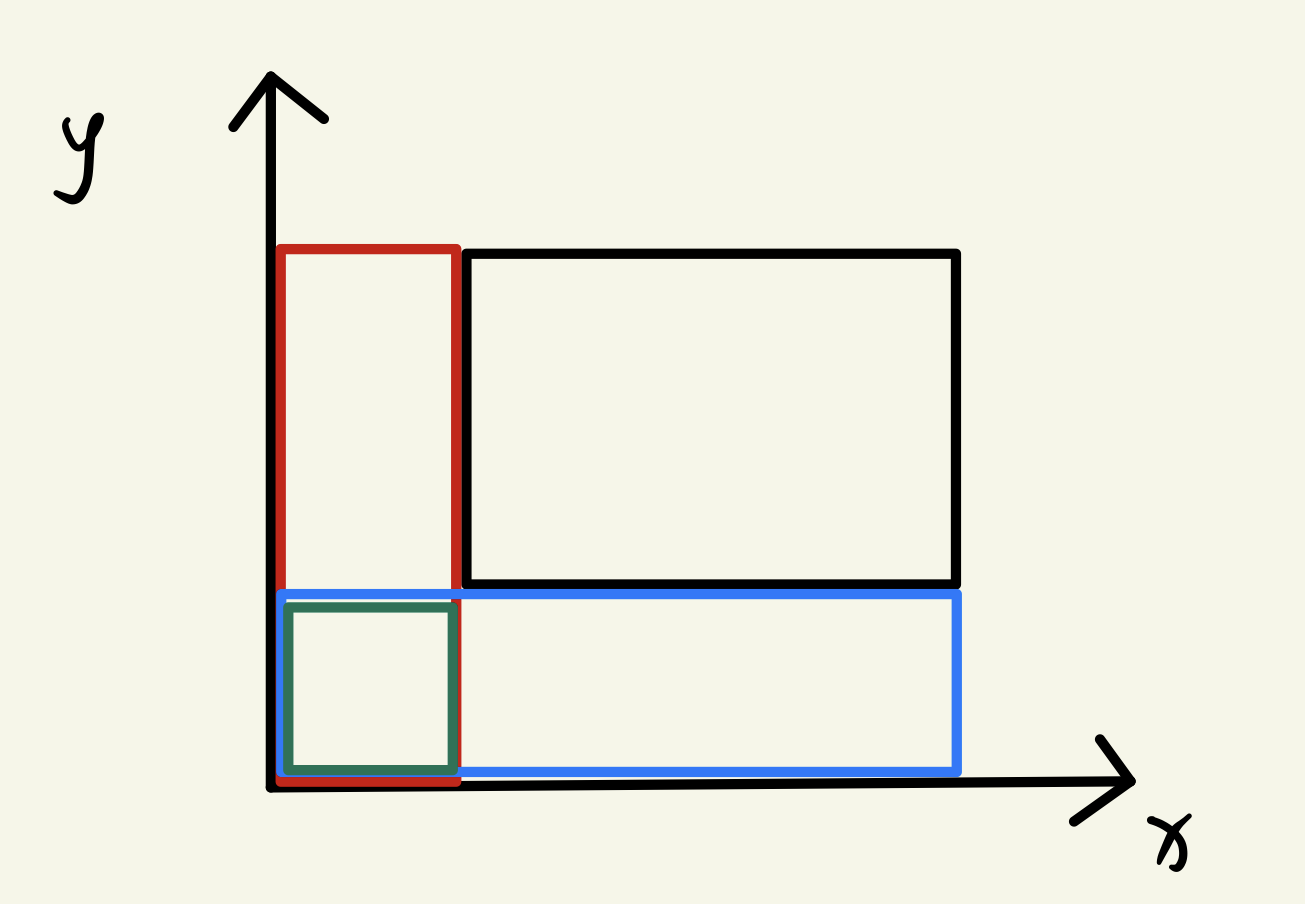
这里的主要思路其实也要用到二维前缀和。我们知道,对于一个矩阵,左下角为 ((x_{1}, y_{1})) ,右上角为 ((x_{2}, y_{2})) ,那么通过二维前缀和,矩阵和就为 (S = s[x_{2}][y_{2}] - s[x_{2}][y_{1} - 1] - s[x_{1} - 1][y_{2}] + s[x_{1} - 1][y_{1} - 1]) 。
那么我们就可以把一个矩阵和分成四部分 (s[x_{2}][y_{2}], s[x_{2}][y_{1} - 1], s[x_{1} - 1][y_{2}], s[x_{1} - 1][y_{1} - 1]) 。
我们就可以离线把这些询问矩阵都存储下来,离散化处理,然后对于每个询问都拆解成四部分。然后通过扫描线从左到右扫 (x) 坐标,并逐一处理所拆解出来的询问,最后就能合出每一个完成的询问结果。
每次通过树状数组来求解前缀和,时间复杂度为 (O(logN)) ,所以处理完所有请求的时间复杂度为 (O(mlogn)) 。
P2163 园丁的烦恼 - 洛谷
有 (n) 个点 ((x, y)) 和 (m) 次查询,对于每次查询要输出以 ((a,b)) 为左下角, ((c, d)) 为右上角的矩形内部有多少点(包括边界)。
#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
typedef pair<int, int> PII;
const int N = 5e5 + 10, M = 1e7 + 10;
vector<PII> v; // 存所有的点坐标
struct Query { // 存所有的被拆分出来询问
// opt = 1, 加值; op5 = -1, 减值
int x, y, id, opt;
bool operator<(const Query &w) { // 重载, x 坐标递增排序
return x < w.x;
}
} Q[N * 4];
int tr[M]; // 树状数组
int ans[N]; // 答案
int n, m;
int lowbit(int x) { return x & -x; }
void add(int x, int c) {
for (int i = x; i < M; i += lowbit(i)) tr[i] += c;
}
int query(int x) {
int res = 0;
for (int i = x; i; i -= lowbit(i)) res += tr[i];
return res;
}
int main() {
cin >> n >> m;
for (int i = 1; i <= n; i++) {
int x, y;
scanf("%d%d", &x, &y);
x++, y++; // 让下标从 (1, 1) 开始, 题目是 (0, 0)
v.push_back({x, y});
}
sort(v.begin(), v.end()); // 坐标排序
int cnt = 0;
for (int i = 1; i <= m; i++) {
int x1, y1, x2, y2;
scanf("%d%d%d%d", &x1, &y1, &x2, &y2);
x1++, y1++, x2++, y2++;
// 根据二维前缀和来拆分请求, 并存储
Q[++cnt] = {x1 - 1, y1 - 1, i, 1};
Q[++cnt] = {x2, y2, i, 1};
Q[++cnt] = {x2, y1 - 1, i, - 1};
Q[++cnt] = {x1 - 1, y2, i, -1};
}
sort(Q + 1, Q + cnt + 1); // 请求排序
int idx = 0;
for (int i = 1; i <= cnt; i++) {
Query q = Q[i];
while (idx < n && v[idx].first <= q.x)
add(v[idx].second, 1), idx++;
ans[q.id] += q.opt * query(q.y); // 单独计算每一部分
}
for (int i = 1; i <= m; i++) printf("%dn", ans[i]);
return 0;
}
Pair Sum and Perfect Square
给定一个 (1 sim n) 的排列,有 (m) 次询问操作。
对于每次询问要输出 ([L, R]) 区间里,对于 (L le i < j le R) ,有多少 (p_{i} + p_{j}) 是平方数。
先预处理出所有能成对构成平方数的 ((i, j)) ,然后将问题转化为求二维矩阵内点的个数。
#include <bits/stdc++.h>
using namespace std;
typedef pair<int, int> PII;
const int N = 1e5 + 10;
struct Query {
int x, y, id, opt;
bool operator<(const Query &w) const {
return x < w.x;
}
} Q[N * 4];
vector<int> Sqrt;
vector<PII> v;
int p[N];
int st[N]; // 位置
int ans[N]; // 答案
int tr[N]; // 树状数组
int n, m;
int lowbit(int x) { return x & -x; }
void add(int x, int c) {
for (int i = x; i <= n; i += lowbit(i)) tr[i] += c;
}
int query(int x) {
int res = 0;
for (int i = x; i; i -= lowbit(i)) res += tr[i];
return res;
}
void init() {
for (int i = 2; i * i < N * 2; i++)
Sqrt.push_back(i * i);
}
int main() {
ios::sync_with_stdio(false);
cin.tie(0);
init();
int T;
cin >> T;
while (T--) {
cin >> n;
for (int i = 1; i <= n; i++) {
cin >> p[i];
st[p[i]] = i;
tr[i] = ans[i] = 0;
}
v.clear();
for (int i = 1; i <= n; i++) {
int x = p[i];
for (auto y : Sqrt) {
if (y - x > n) break;
if (y <= x) continue;
if (st[y - x] > i)
v.push_back({i, st[y - x]});
}
}
cin >> m;
int cnt = 0;
for (int i = 1; i <= m; i++) {
int l, r;
cin >> l >> r;
Q[++cnt] = {r, r, i, 1};
Q[++cnt] = {l - 1, l - 1, i, 1};
Q[++cnt] = {l - 1, r, i, -1};
Q[++cnt] = {r, l - 1, i, -1};
}
sort(Q + 1, Q + cnt + 1);
int idx = 0;
int len = v.size();
for (int i = 1; i <= cnt; i++) {
Query q = Q[i];
while (idx < len && v[idx].first <= q.x)
add(v[idx].second, 1), idx++;
ans[q.id] += q.opt * query(q.y);
}
for (int i = 1; i <= m; i++) cout << ans[i] << "n";
}
return 0;
}
参考资料
文章来源: 博客园
- 还没有人评论,欢迎说说您的想法!




 客服
客服


