Burnside 定理

问题：

给定一个 (n) 个点，(n) 条边的环，有 (m) 种颜色，给每个顶点染色，问有多少种本质不同的染色方案，答案对 (10^9+7) 取模

注意本题的本质不同，定义为：只需要不能通过旋转与别的染色方案相同。

题目初步解读

我们考虑如果不要求本质不同只需要 (n^n) 。

但因为无标号的环就会重复。

例如这是一个 4 个点， 2 种颜色的情况：

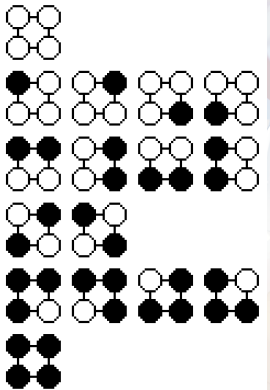
在这里面如果不要求本质不同就有 16 种方案，若要求，则只有 6 种。

同一行的都是一种方案。

Burnside 引入

我们先来一些定义

置换群

令集合 (N={1,2,cdots,n}) 。

令集合 (M) 为 (N) 若干个排列构成的集合。

令群 (G = (M,times)) 其中符号 (times) 解释如下：

(sigma) 是一个排列，也就是 (M) 周一个元素。

写为 (sigma times a) 不过更习惯被表示为 (sigma(a)) 。

其运算规则为：(sigma(a)= (a_{sigma_1},a_{sigma_2}...a_{sigma_n}))。

在前面样例中，置换群是：

(({)旋转(0°,)旋转(90°,)旋转(180°,)旋转(270° },times))

若写成排列则是：

(({{1,2,3,4},{2,3,4,1},{3,4,1,2},{4,1,2,3}},times))

轨道

考虑一个作用在 (X) 上的置换群 (G) ， (X) 中一个元素 (x) 的轨道则是 (x) 通过 (G) 中元素可以转移到的元素的集合。记作 (G(x)) 。

样例中每一行就是一个轨道。例如下面就是一个轨道。

稳定子

稳定子定义为：(G^x = {g|gin G,g times x = x})。

使用语言描述，便是群 (G) 中满足 (g(x)=x) 的所有元素 (g) 所构成的集合。

样例中：
的稳定子为 ({)旋转(0°})，
的稳定子为 ({)旋转(0°,)旋转(180°})，
的稳定子为 ({)旋转(0°,)旋转(90°,)旋转(180°,)旋转(270°})。

轨道-稳定子定理：

我们可以发现：

1.在同一轨道的元素稳定子个数一定相等。

2.稳定子大小乘轨道大小等于群 (G) 大小。

没错，他是个定理，考虑感性证明：

一个元素 (x) 按照 (G) 的操作一定可以得到轨道内所有元素，也就是集合 (G(x)) 。

但在操作过程中会有重复的，重复的次数也就是稳定子集合大小。

详细证明可以看这里。

不动点

若 (g(x) = x) 则称 (x) 是在 (g) 下的不动点。

定义集合 (X^g = {x|g(x) = x,xin X})。

稳定子和不动点有类似反演的关系。

若 x 的稳定子集合里有 (g)，那么 g 下不动点集合中也有 x。

所以对于每一个 (x) 稳定子的个数之和等于对于每一个 (g) 不动点个数之和。

形式化

注意稳定子是对于 g 来说的，而不动点是对于 x 来说的。

例如 ''旋转180°'' 不动点是

Burnside 定理

公式：

我们要求的答案一般来说也就是轨道数量。

证明：

等价类数量也就是轨道数量。

(|G(x)|) 代表 (x) 所在轨道大小。

根据轨道-稳定子定理得

用稳定子和不动点关系得：

回到题目

扩展到 (n)，现在的 (G) 就是({) 旋转 (0) 次，旋转 (1) 个，(cdots)，旋转(n-1)个 (})。

考虑旋转 (k) 次的不动点个数是 (n^{gcd(k,n)})。

当 (gcd(k,n) = k):

我们按照 (k) 将环切成 (frac n k) 份，然后标上号。

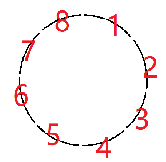
将他旋转。

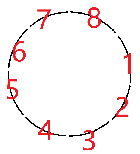
我们发现每一份必须一样他才是个不动点。

答案就是 (n^k = n^{gcd(n,k)})。

当 (gcd(k,n) ne k):

令 (g = gcd(k,n)) 那么我们将他旋转 (g times frac k g) ，等价于将长度为 (g) 的旋转 (frac k g) 次。

答案就是 (n^{gcd(n,k)})。

如果还不懂，建议手模一下 (k = 4,n = 6) 这个样例。

应用Burnside则有

发现有 (gcd) ，可以莫反。

莫反基操，不多说。

直接暴力可过。

Pólya 定理

就是染色问题中Burnside的运用。

对于一个排列 (g) ，我们将每一个 (i) 向 (a_i) 连一条边，会得到若干环，每个环内元素颜色应该相同。定义 (c(g)) 代表环数量，那么 Pólya 就是

• 还没有人评论，欢迎说说您的想法！