关系型数据库-关系操作集合
1、 基本的关系操作
关系模型中常用的关系操作包括查询(Query)操作和插入(Insert)、删除 (Delete)、修改(Update)操作两大部分。
查询操作分为:选择、投影、连接、除、并、差、交、笛卡尔积等;
五种基本操作:选择、投影、并、差、笛卡尔积;
关系操作的特点是集合操作方式,即操作的对象和结果都是集合、这种操作方式也称为一次一集合的方式。
2、关系数据语言的分类
关系操作是通过关系语言来实现的。 关系语言的特点是高度非过程化,即:
(1)用户不必请求数据库管理员为其建立特殊的存取路径,存取路径的选择由 DBMS 的优化机制来完成;
(2)用户也不必求助于循环和递归来完成数据的重复操作。
关系操作的能力可以用两种方式来表示:代数方式和逻辑方式。 关系代数、元组关系演算和域关系演算均是抽象的查询语言。结构化查询语言SQL充分体现了关系数据语言的特点和优点,是关于数据库的标准语言。
关系数据语言可以分为三类:关系代数语言、关系演算语言以及兼具两者双重特点的语言。三类语言的共同特点是语言具有完备的表达能力,是非过程化的集合操作语言,功能强,能够独立使用也可以嵌入高级语言中使用。
3、 关系代数
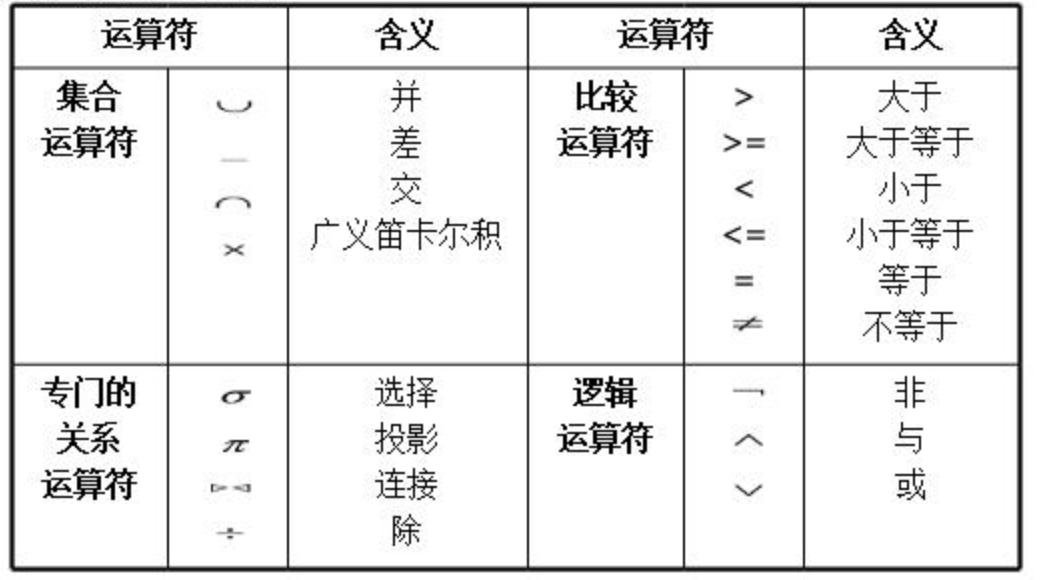
操作包含三大要素:操作对象、操作符、操作结果。在关系代数操作中,操作对象和操作结果均为关系。 关系代数直接应用关系的运算来表达操作目的,而代数用到的运算符包括集合运算符合专门的关系运算符两类,如下表所示:
(关系代数运算符)
A. 传统的集合运算是二目运算,关系看成元组的集合,其运算关系是从关系的“水平”方向,即行的角度来进行,有并、差、交、笛卡尔积 4 种运算。
1. 并:假设有两个关系 R1 和 R2,R1 和 R2 的并运算产生一个新关系 R3。R3 是 由属于关系 R1 或 R2 的所有不同元组所组成,记为 R3=R1∪R2。
2. 差:假设有两个关系 R1 和 R2,R1 和 R2 的差运算产生一个新关系 R3。R3 是由属于关系关系 R1,但不属于 R2 的元组组成,记为 R3=R1-R2。
3. 交:假设有两个关系 R1 和 R2,R1 和 R2 的交运算产生一个新关系 R3。R3 是由既属于关系 R1,同时又属于 R2 的元组组成,记为 R3=R1∩R2。
4. 笛卡尔积:假设有两个关系 R1 和 R2,且 R1 为 m 元关系,R2 为 n 元关系, R1 和 R2 的笛卡尔积产生一个新关系 R3,记作 R3=R1✖R2。R3 是 由 R1 和 R2 的所有元组连接而成的具有(m+n)个分量的元组组成。
B. 从列的角度,可分为一元专门关系操作和二元专门关系操作。 一元专门关系操作包括对单个关系进行垂直分解的投影运算和进行水平分解选择运算;二元专门关系操作则是对两个关系进行操作,包括连接运算和除运算。
(0)相关概念:
(0.0)域是一组具有相同数据类型值的集合。
(0.1)设关系模式为R(A1, A2, …, An)。它的一个关系设为R。t∈R表示t是R的一个元组。t[Ai]则表示元组t中相应于属性Ai的一个分量 。
(0.2)给定一个关系R(X,Z),X和Z为属性组。我们定义,当t[X]=x时,x在R中的象集(Images Set)为:
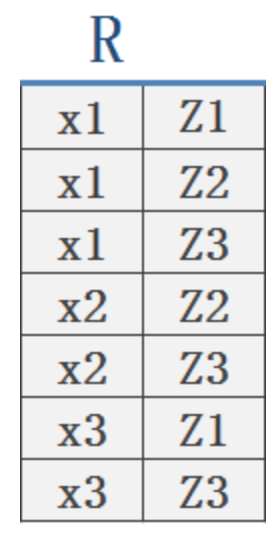
eg:如下图所示关系R,则
x1在R中的像集Z(x1)={Z1,Z2,Z3},
x2在R中的像集Z(x2)={Z2,Z3},
x3在R中的像集Z(x3)={Z1,Z3}。
注:以下举例统一使用,设存在Student表,Sno表示学号属性,Sage表示年龄,Sname表示姓名,Ssex表示性别,Sdept表示所在系
(1) 选择(SELECT)
选择运算表示为: ![]()
其中,F 为条件表达式,R 为指定的被运算关系名。
sql伪代码形式如下:
SELECT 关系名 WHERE 条件
eg:
则查询表中年龄小于20的学生,
关系代数方式:
SQL方式: select * from Student where Sage > 20 (2) 投影(PROJECTION)
关系R上的投影是从R中选择出若干属性列组成新的关系。记作:![]() 其中A为R中的属性列。投影操作是从列的角度进行运算。
其中A为R中的属性列。投影操作是从列的角度进行运算。
eg:
查询学生的姓名和所在系,即求Student关系上学生姓名和所在系两个属性上的投影
关系代数方式: ∏Sname,Sdept(Student)
SQL方式: select Student.Sname,Student.Sdept form Student
注意:投影之后不仅取消了原关系的某些列,而且还可能取消某些元祖,因为取消了某些属性之后,就可能出现重复行,应取消这些完全相同的行。
(3) 连接(JOIN)
连接运算也称为θ连接,从两个关系(R、S)中的广义笛卡尔积中选取属性间满足一定条件的元组形成一个新的连接:
其中: A为包含R中的属性的表达式;
B为包含S中的属性的表达式;
θ通常为关系比较符。
(3.1) 非等值连接
θ不为“=”的连接称为非等值连接
sql伪代码: select * from emp e join dept d on e.sal > d.avgsal
(3.2) 等值连接
θ为“=”的连接称为等值连接,它是从关系R和S的笛卡儿积中选取A、B属性值相等的那些元组。等值连接的属性名可以相同也可以不相同。
select * from emp e join dept d on e.sal = d.avgsal
select * from emp e join dept d on e.deptno = d.deptno
(3.3) 自然连接
自然连接是一种特殊的等值连接,它要求两个关系进行比较的分量必须是同名的属性组,并且在结果中把重复的属性列去掉。一般的连接是从行的角度进行操作,自然连接需要取消重复列,所以它是从行和列的角度进行操作。
select * from emp natural join dept
(3.4) 外连接
两个关系R和S在做自然连接时,选择两个关系在公共属性上值相等的元组构成新的关系。此时,关系R和S可能有在公共属性上不相等的元组,从而造成R或S中元组的舍弃,这些舍弃的元组被称为悬浮元组。如果把悬浮元组也保存在结果关系中,而在其他属性上填空值,那么这种连接就叫做外连接。
① 左外连接
如果只保留左边关系R中的悬浮元组就叫做左外连接。
select * from emp e left join dept d on e.deptno = d.deptno --员工8888没有部门,只保留左表的悬浮元组,其他属性为null
② 右外连接
如果只保留右边关系S中的悬浮元组就叫做右外连接。
select * from emp e right join dept d on e.deptno = d.deptno --40号部门没有人,只保留右表的悬浮元组,其他属性为null
③ 全外连接
如果保留两边关系R和S中的所有悬浮无级就叫做全外连接。
select * from emp e full join dept d on e.deptno = d.deptno --保留两边的悬浮元组,左表和右表各有一条悬浮元组记录,一共16行
(3.5) 自连接
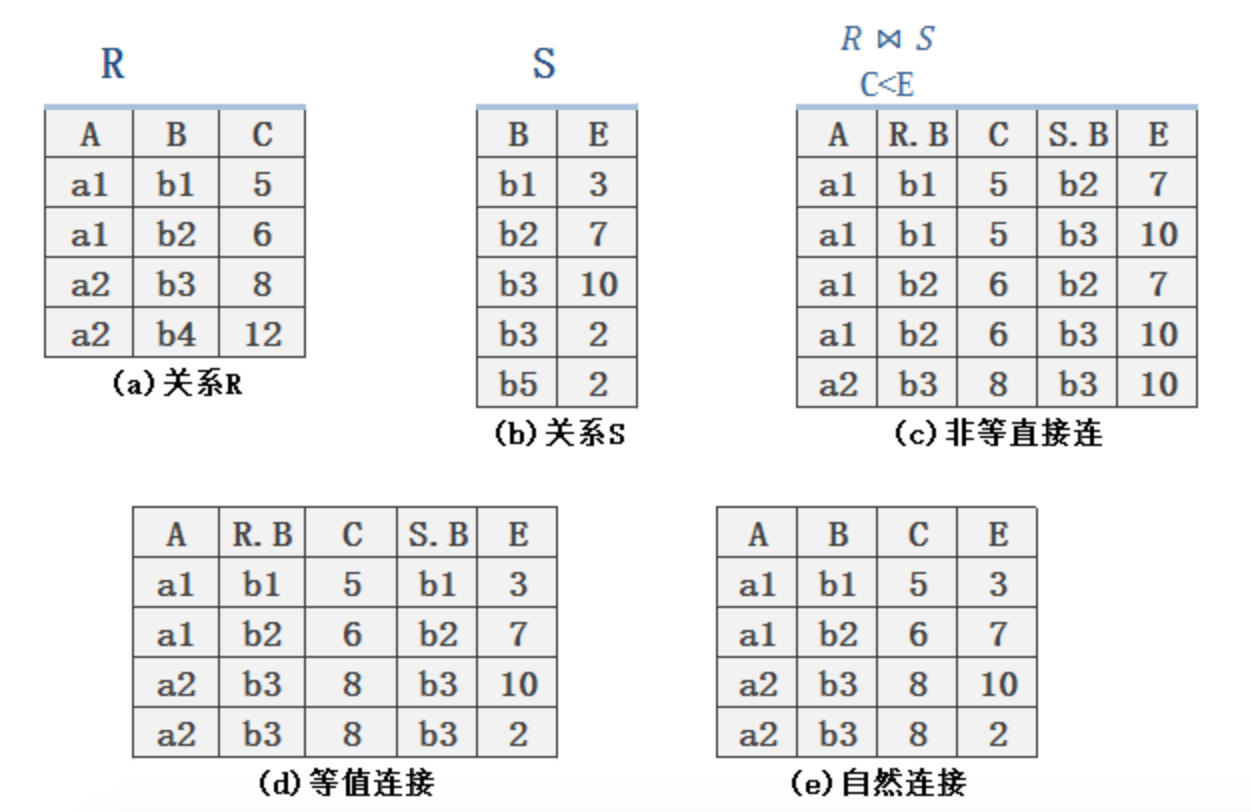
select * from emp e1 join emp e2 on e1.empno = e2.mgr 设图中(a)和(b)分别是关系R和关系S,图中(c)为非等值连接的结果,图(d)为等值连接
的结果,图(e)为自然连接
的结果:
(4) 除(DIVISION)
除运算表示为: R➗S,其中 R 和 S 代表两个不同的关系。在除运算中,若被除关系为 m 元关系,除关系为 n 元关系,则运算结果为一个 m-n 元关系。
用象集来定义除法:
① 给定关系R(X,Y)和S(Y,Z),其中X、Y、Z为属性组,R中的Y与S中的Y可以有不同的属性名,但必须出自相同的域集;
② 元组在X上的分量值x的象集K要包含S在Y上投影的集合,满足前面条件的元组在X属性上的投影就是R除以S的结果关系;
③ 除操作是同时从行和列角度进行的操作。
关系R
| X | Y |
| x1 | y1 |
| x1 | y1 |
| x1 | y2 |
| x2 | y3 |
| x2 | y5 |
关系S
| Y | Z |
| y1 | z1 |
| y3 | z2 |
R÷S
| X |
| x1 |
分析:
① S在(Y)上的投影的集合是:{(y1),(y3)};
② 元组在X上的分量值x的象集有两组;
x1的象集K1={(y1),(y2),(y3)}
x2的象集K2={(y3),(y5)}
③ 从①②得知只有象集K1包含了S在(Y)上的投影;
④ 满足以上条件的象集K1在X属性上的投影为{(x1)}。
非常感谢您的阅读,如需转载请注明出处,本文链接https://www.cnblogs.com/huyangshu-fs/p/11624939.html
另附推荐相关博客链接https://blog.csdn.net/Alexshi5/article/details/80024250
- 还没有人评论,欢迎说说您的想法!



 客服
客服


