Convex Hull 实现理论

789 0 0

作者:Hamilton算符

Convex Hull

概述

计算n维欧式空间散点集的凸包，有很多的方法。但是如果要实现快速运算则其难点在于：如何快速判断散点集的成员是否是在凸集的内部。如果可以简化判断的运算过程，则可以极大简化迭代过程中的运算负荷。下面简述一下我用单纯形做的一个在高维欧式空间下模仿分形绘制过程快速实现Convex Hull函数的算法。

点的位置判断
假定已知n维欧式空间的单纯形S，S以为顶点，b为任意点，，现在想要判断b是否在n维单纯形S的内部。

根据超平面分离定理，点和b在所在的超平面的同一侧当且仅当：

将第一个式子代入第二个式子即有：

进一步变形有：

根据单纯形的构造可知，b在S的内部当且仅当：

算法
已知n维欧式空间的散点集，U的凸包为H，目标是算出和并且提供视觉上的可绘制方案。

　　现在我们考虑散点集的特殊情况。若且以为顶点可以构成n维单纯形S，那么问题变得很简单，显然有：

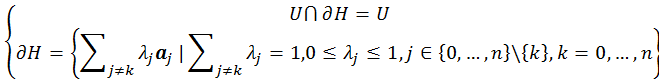
　　对于一般的散点集而言我们仍然可以这么做，但是需要改造一下。这里我设计了容器B：

　　B: 字典形式，U上的维单纯形的顶点-->上的到此单纯形直线距离最短（距离可以是负数）的点。

　　算法具体步骤如下：

Step1.找出中可以组成单纯形的n-1个点，对的排序进行调整，使得：

初始化B：

并设计一个空列表C:

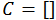
Step2.关于，解以下问题：

如果有解p，则将p添加到列表C中：

Step3.循环Step2直至遍历了B上的所有元素，构造集合D：

这里在构造D做并运算的时候，将排序奇偶性不相同的2个元素视作同1个元素，将排序奇偶性相同的2个元素视作不同的2个元素（这里没错，如果你深入学习过单纯形的理论，应该大致可以理解此处的用意）。

考虑集合D和集合B的之间关系，再次用上面描述的交运算对B进行update：

Step3.循环Step2-4直至对于B中的任意元素都有Step2中的问题都无解为止。此时：

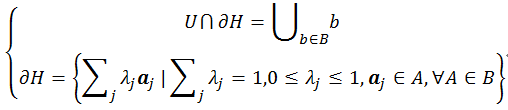
注：算法里有很多可以升级，我写的升级之后以后的算法可以大幅度降低计算量。但是为了让读者更加轻松的理解该算法根本原理，这里笔者还是觉得应该用最初的构思框架来描述。

python代码试验
　　测试的例子可以是任意维数的，不过超过3维的数据是无法视觉显示的，所以这里只展示2个3维凸包的例子：

ex_1：

from MyClass import *
import numpy
from mpl_toolkits.mplot3d import Axes3D
import matplotlib.pyplot as plt


M = numpy.array([[6, 0, 9, 9, 6, 6, 2, 0, 6, 5, 7, 2, 6, 7, 3, 7, 4, 4],
                 [5, 7, 2, 6, 7, 3, 7, 4, 4, 6, 0, 9, 9, 6, 6, 2, 0, 6],
                 [8, 3, 2, 5, 0, 0, 7, 6, 5, 9, 6, 6, 2, 0, 6, 5, 0, 0]])
obj = ConvexHullMap(matrix=M)
print("obj.points = ", obj.points, 'n')

fig = plt.figure()

sub = [331, 332, 333, 334, 335, 336, 337, 338, 339]
ax = list()
for j in range(0, len(sub)):
    ax.append(fig.add_subplot(sub[j], projection='3d'))
    ax[j].scatter(M[0, :], M[1, :], M[2, :])
    for k in range(0, 9):
        ax[j].text(M[0, k], M[1, k], M[2, k], s=str(k))
    for patch in obj.patches:
        matrix = obj.all[:, patch]
        X = [matrix[0, 0], matrix[0, 1], matrix[0, 2], matrix[0, 0]]
        Y = [matrix[1, 0], matrix[1, 1], matrix[1, 2], matrix[1, 0]]
        Z = [matrix[2, 0], matrix[2, 1], matrix[2, 2], matrix[2, 0]]
        ax[j].plot(X, Y, Z)

    obj.classify_points()
    if obj.next_points.count(None) == len(obj.next_points):
        break
    print(obj.next_points)
    obj.expand_patches()

plt.show()

上面一段代码的意思是绘制

M = numpy.array([[6, 0, 9, 9, 6, 6, 2, 0, 6, 5, 7, 2, 6, 7, 3, 7, 4, 4],
                 [5, 7, 2, 6, 7, 3, 7, 4, 4, 6, 0, 9, 9, 6, 6, 2, 0, 6],
                 [8, 3, 2, 5, 0, 0, 7, 6, 5, 9, 6, 6, 2, 0, 6, 5, 0, 0]])

M的凸包的前9步的结果，图形如下：

累次打印的结果：

当最后打印的列表全部元素均为None时，说明此时凸包计算完毕应当终止迭代。

ex_2:

from MyClass import *
import numpy
from mpl_toolkits.mplot3d import Axes3D
import matplotlib.pyplot as plt


M = numpy.array([[6, 0, 9, 9, 6, 6, 2, 0, 6],
                 [5, 7, 2, 6, 7, 3, 7, 4, 4],
                 [8, 3, 2, 5, 0, 0, 7, 6, 5]])
obj = ConvexHullMap(matrix=M)
print("obj.points = ", obj.points, 'n')

fig = plt.figure()

sub = [331, 332, 333, 334, 335, 336, 337, 338, 339]
ax = list()
for j in range(0, len(sub)):
    ax.append(fig.add_subplot(sub[j], projection='3d'))
    ax[j].scatter(M[0, :], M[1, :], M[2, :])
    for k in range(0, 9):
        ax[j].text(M[0, k], M[1, k], M[2, k], s=str(k))
    for patch in obj.patches:
        matrix = obj.all[:, patch]
        X = [matrix[0, 0], matrix[0, 1], matrix[0, 2], matrix[0, 0]]
        Y = [matrix[1, 0], matrix[1, 1], matrix[1, 2], matrix[1, 0]]
        Z = [matrix[2, 0], matrix[2, 1], matrix[2, 2], matrix[2, 0]]
        ax[j].plot(X, Y, Z)

    obj.classify_points()
    if obj.next_points.count(None) == len(obj.next_points):
        break
    print(obj.next_points)
    obj.expand_patches()

plt.show()

上面一段代码的意思是绘制

M = numpy.array([[6, 0, 9, 9, 6, 6, 2, 0, 6],
                 [5, 7, 2, 6, 7, 3, 7, 4, 4],
                 [8, 3, 2, 5, 0, 0, 7, 6, 5]])

M的凸包的前9步的结果，图形如下：

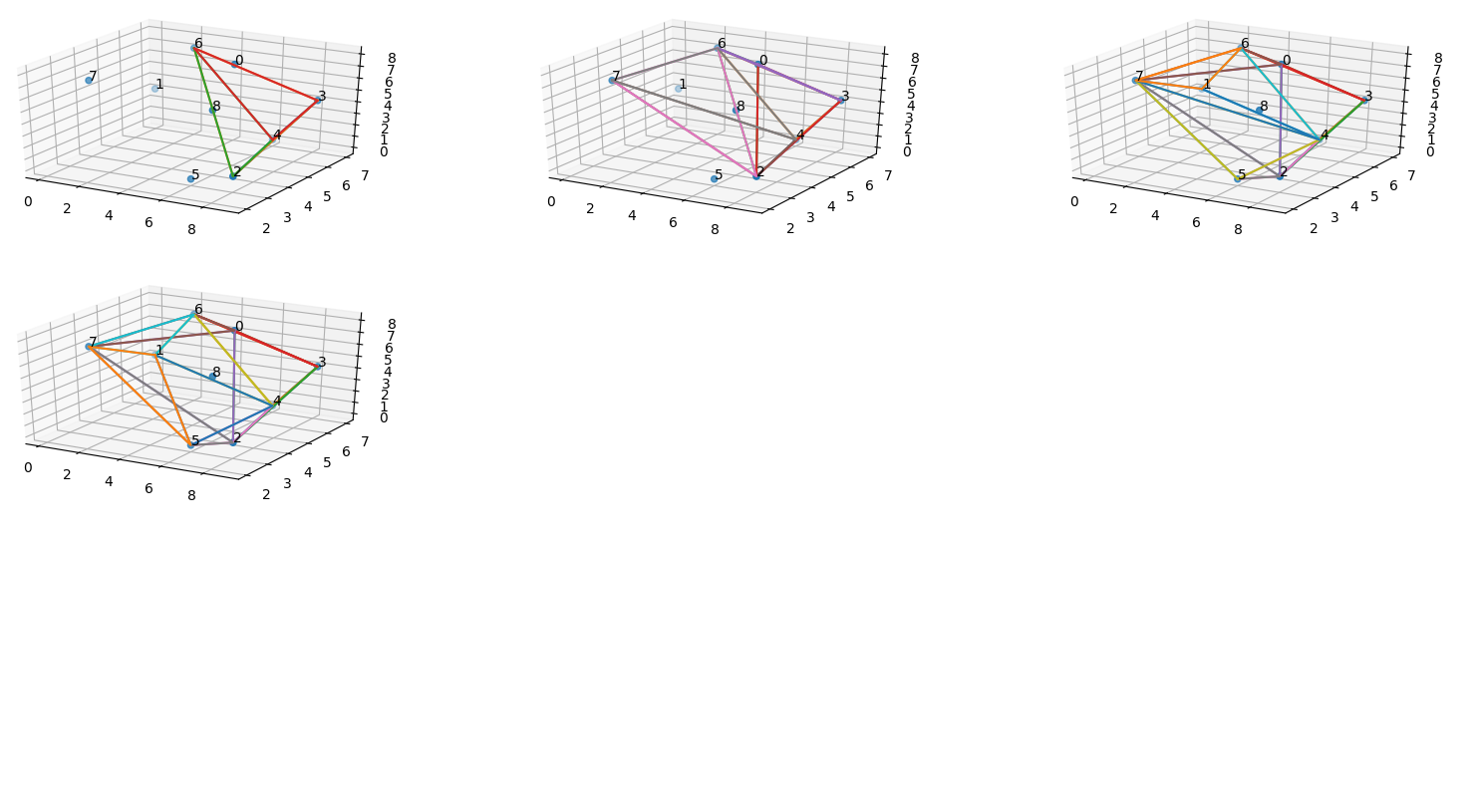
显然到了第4步就已经完成了凸包的计算。并且有一个下标是8的点是凸包的内点。

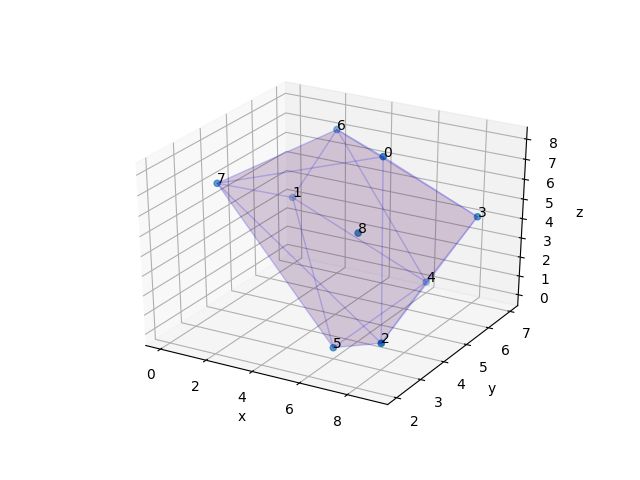
ex_3:

from MyClass import *
import numpy
from mpl_toolkits.mplot3d import Axes3D, art3d
import matplotlib.pyplot as plt


M = numpy.array([[6, 0, 9, 9, 6, 6, 2, 0, 6],
                 [5, 7, 2, 6, 7, 3, 7, 4, 4],
                 [8, 3, 2, 5, 0, 0, 7, 6, 5]])
obj = ConvexHullMap(matrix=M)
obj.complete()

fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
ax.set_xlabel("x")
ax.set_ylabel("y")
ax.set_zlabel("z")

ax.scatter(M[0, :], M[1, :], M[2, :])
for k in range(0, 9):
    ax.text(M[0, k], M[1, k], M[2, k], s=str(k))

tri = []
for patch in obj.patches:
    matrix = obj.all[:, patch]
    matrix = matrix.T
    tri.append(matrix)

patches = art3d.Poly3DCollection(tri, array=numpy.zeros(len(tri)))
patches.set_alpha(0.1)
patches.set_edgecolor("b")
ax.add_collection(patches)
ax.autoscale()
plt.show()

结果显示一个透视的图：

声明

本文由“Hamilton算符”原创，未经博主允许不得转载！

内容来源于网络如有侵权请私信删除

标签：算法数据结构

你还没有登录，请先登录或注册！

还没有人评论，欢迎说说您的想法！

Convex Hull 实现理论