1. 对数坐标图
(1)概念引出
研究频率,一定会用到对数坐标图,对数图可以表现很宽范围内的频率的相对变化对电路性能的影响,而且这种效果是普通的线性坐标图达不到的。
这样说可能有点抽象,我们举个现实中关于消费的例子你可能就理解了。比如,如果你要买个馒头,馒头的价格若是从1块钱涨到5块,你可能就觉得贵了;接下去,你打算买个手机,如果手机的价格变化个5块钱,你可能完全不在乎,在买手机的情况下,你在乎的是几百块到几千块上下的价格变化;再接下去,你如果打算要买辆汽车,汽车的价格若是变化个几百块,对你来说可能也完全不上心了,你在乎的是万元级的价格上下变化。
买汽车时的几百块、和买手机时的几百块、和买馒头时的几块钱,它们的客观单位是一样的,都是“元”,但是对你的心理来讲,在不同的价位区间时对它们的评估标准是不一样的。这个就是对数坐标图能大显身手的地方,它能在不同的区间体现“相对变化”带来的影响。
(2)对数坐标图的特性
对数坐标将原数值取对数后,再将这个对数结果按比例分配到坐标轴上,常用的对数坐标通常以10为底,也有时候会以2为底和以e为底,这种情况一般会在图旁边特别说明。
对数坐标图有“半对数坐标图”和“全对数坐标图”两种。半对数坐标图的横坐标为对数坐标,纵坐标仍为普通坐标;而全对数坐标图的纵坐标和横坐标都为对数,此图有一个变种,即纵坐标为分贝表示(分贝也是对数的一种),分贝图我们放到下一小节再看。本小节我们先关注普通对数坐标图的一些特性,下图为一个半对数坐标图横坐标从1到10的图例:

图10-1.01
从图上可以看到,横坐标从1变化到2时,占据了大约30%的跨度,从1到3占据了大约一半的跨度,从1到5占据了大约70%的跨度,而从9到10仅占据了不到%5的跨度。这点很符合我们先前的直觉,价格从1块变到2块我们会比较关注,但从9块变到10块我们可能就不那么关注了。
然后我们再将横坐标的范围放大到1~1000的范围,如下图所示:
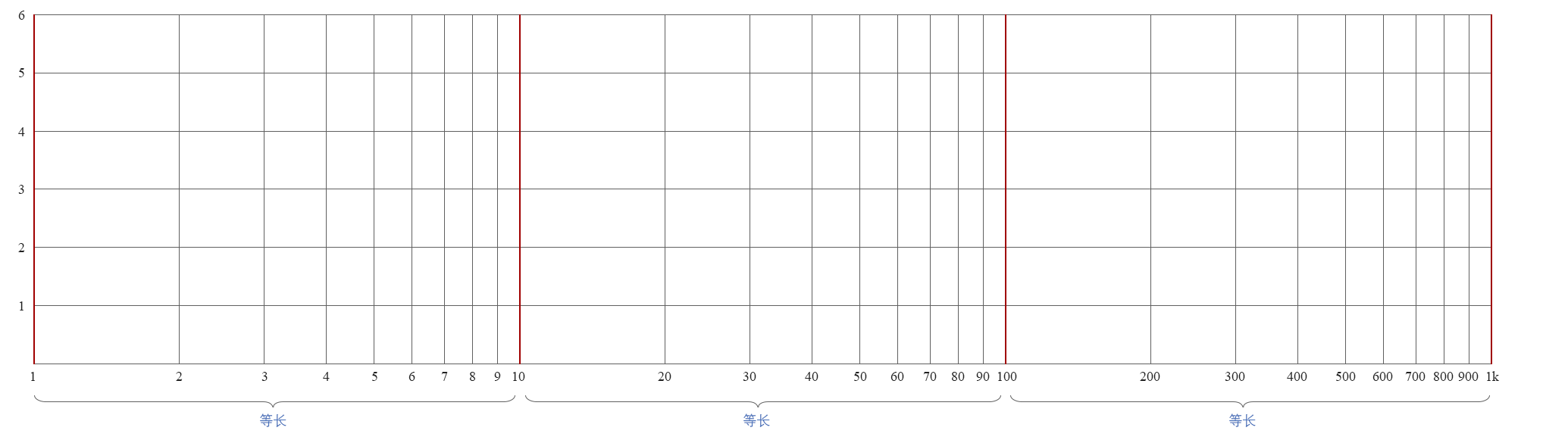
图10-1.02
从图上可以看到,从1~10和从10~100和从100~1k,它们的横坐标长度是等长的,也就是说,横轴数值每增加10倍,它们在图上所占据的跨度是相同的。这是对数坐标图的一个重要特性!
横坐标数值不仅可以往大增加范围,还可以往小增加范围,如果你要研究小尺度的问题,同样可以将对数坐标向左无限扩展,每缩小10倍,它们在图上的跨度仍旧是相同的,下图是0.01~10的范围的对数坐标图:
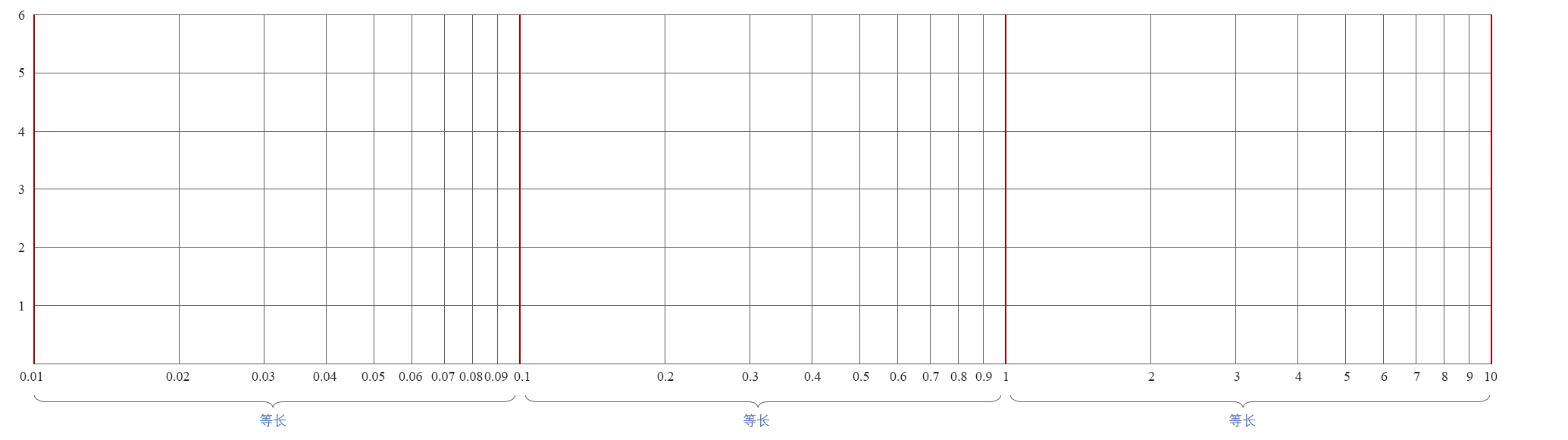
图10-1.03
一般在使用对数坐标图的时候,我们仅需要取我们关注的横坐标范围就可以了(比如0.1~10,或是1~10000等),向左可以无限扩展(永远不会到达0),向右也可以无限扩展(永远不会到达无穷大)。
最后,在使用对数坐标图做图解法求值的时候,需要把图上量到的尺寸,再用反对数计算变回去得到原值,方法如下:

图10-1.04
当你需要计算A点横坐标的实际数值时,先在图上量出A点到10x的距离为da,然后再量出10x到10x+1的尺寸为D(回顾一下:每个10倍跨度都是等长的),则A点的实际数值的计算公式为:
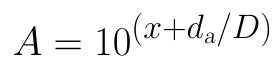
(3)十倍程
最后再讲一个使用对数图时经常出现的单位:十倍程(decade)。
在普通的线性坐标系上,一般横坐标的单位量度是1。比如对于下图的线性坐标和直线y=kx+C:
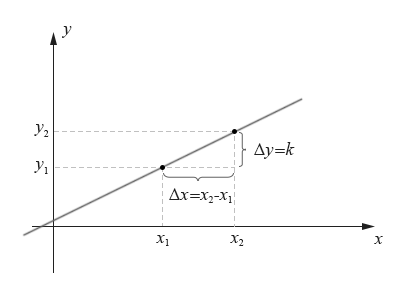
图10-1.05
x每增加1个单位(从x1到x2),y就增加k(Δy=k*1=k),写成表达式就是:

那么问题来了:在对数图上,横坐标的1个单位是多少?由于横坐标的尺度已经变成了lg(x),因此,设设对数图上两个点的横坐标分别为x1和x2,那么横坐标的1个单位就是:
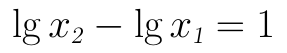
根据对数的性质,可得:
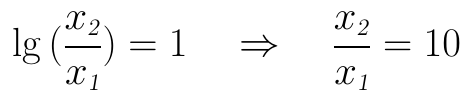
从上式结果可见,对数图上横坐标的1个单位的距离为10倍数值,比如:从1到10、从2到20、从30~300等等,只要x2是x1的十倍,在对数图横坐标上就是一个单位。
在电路的分析中,经常会将频率作为对数图的横坐标,常会出现:“n / 十倍频程” 的说法,意思就是:作为横坐标的频率每增加10倍,纵坐标增加n。
根据上面的lg(x2/x1)的式子,还可看到,只要x2/x1的比值相等,它们在对数横坐标上的距离就是相等的。 比如:从1→2、从3→6、从100→200,它们之间的比值都为2,因此在对数横坐标上的距离也都是相等的。如果用于描述频率,就可以说成:m / 二倍频程,意思是:作为横坐标的频率每翻个倍,纵坐标增加m。
2. 分贝与增益
(1)功率增益
分贝单位是一个电子电路或信号处理中的一个常用单位,不过它的定义可能会令初学者感到有点困惑,尤其不理解那个系数20是怎么来的,所以这里需要把前因后果讲一讲。在了解了这个前后过程后,你会发现分贝这个单位还是挺好用的。
贝尔(bel)这个单位是以纪念电话的发明者贝尔而命名的,最初这个单位的用途是在通信系统中用来衡量功率的增益,其定义为:
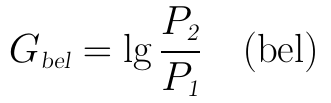
回想一下19世纪末20世纪初那个时代,那时还没有现代信息理论啥的,当时的人们觉得,通信就是远距离传输功率,只要功率大了什么都好办,功率越大,其抗干扰能力就越强、也更能经得起传输的过程中的各种衰减。因此功率的比值是一个很重要的单位:
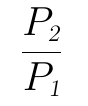
后来人们发现这个比值数字经常太大或太小,在衡量功率放大时经常出现10000、100000等大数、在衡量功率衰减时经常出现0.01、0.001等很小的数字,用起来不方便,于是在前面加了个对数lg,这个就是贝尔的定义公式。这样用起来就清爽很多了,比如:功率放大1000倍是3bel,功率衰减到0.001倍是-3bel。
再后来,人们发现这个单位用起来仍有一点不爽,比如,放大1000倍是3贝尔、放大5000倍是3.7贝尔,放大10000倍是4贝尔。虽然从1000倍到5000倍已经是挺大的变化尺度了,但是在贝尔值尺度上从3到3.7仅仅增加了0.7,有点轻描淡写的感觉。于是人们又定义了一个更细分的单位:分贝(dB),1个贝尔等于10个分贝,分贝值等于原来的贝尔值乘以10。这样一来,放大1000倍就是30dB,放大5000倍就是37dB,增加了7个分贝,于是人们主观上的感觉就好受多了(汗……)。分贝的定义式为:
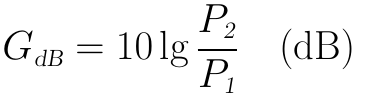
需要注意的是,以上仅仅是关于“功率增益”的分贝表达式,关于电压增益的分贝表达式是不同的,还要看下文。
(2)电压增益
渐渐地,人们发现很多应用情况下并不一定需要放大功率,只要放大电压信号或电流信号就可以了,于是需要一个用来表达电压增益的对数单位。由于分贝这个单位已经广为使用,那么利用功率和电压的换算关系,可以直接利用原来的分贝单位而不用发明新的单位,看下图:
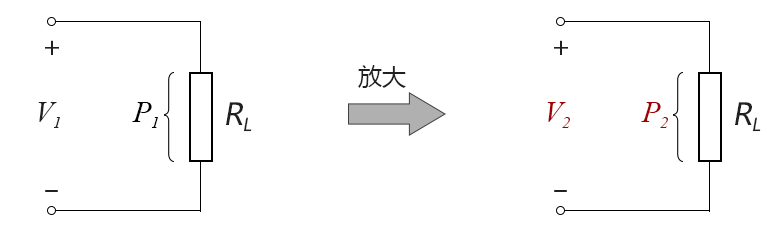
图10-1.06
当电压从V1增大到V2时,在负载RL不变的情况下,功率从P1增大到P2,那么功率和电压的关系式应为:

将其代入前面分贝的表达式:
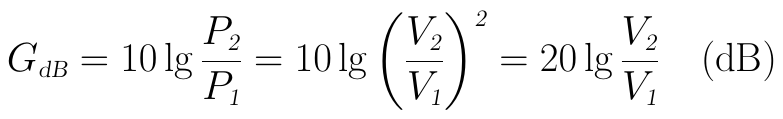
因此,用分贝来表示“电压”的增益时,前面的系数就变为了20。再后来,当人们渐渐用习惯了这个表示电压增益的分贝单位后,连“增益前后电路的RL相等”这个条件都不看了,只是纯粹地使用上面这个公式来表示电压增益,比如在下图中,
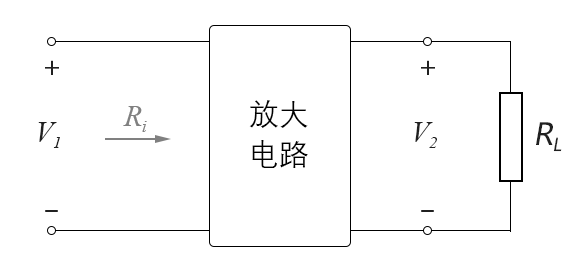
图10-1.07
电压信号V1经过放大电路被放大成V2,虽然从V1处端看入的输入电阻Ri与V2的负载电阻RL完全不同,但人们仍然使用上面的分贝电压增益表达式来表示电压增益。
同理,分贝表示的电流增益的也是如此,其表达式为:
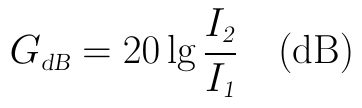
逐渐地,在电子电路系统中,人们更多地使用分贝来表示电压或电流的增益,反而不怎么用来表示功率增益了。
再后来,由于分贝这个单位是如此好用,人们就开始滥用了,将所有的比值(增益或衰减)全都不分青红皂白地分贝单位来表示。比如,对于“频率”这种完全与功率无关的物理量,如果一个电路经过某种改善设计,其带宽频率从1kHz增加到10kHz,人们也会说,其带宽增加了20dB(意思就是带宽增加了10倍),诸如此类……
下表是几个常见的分贝数值和增益倍数的对应关系:
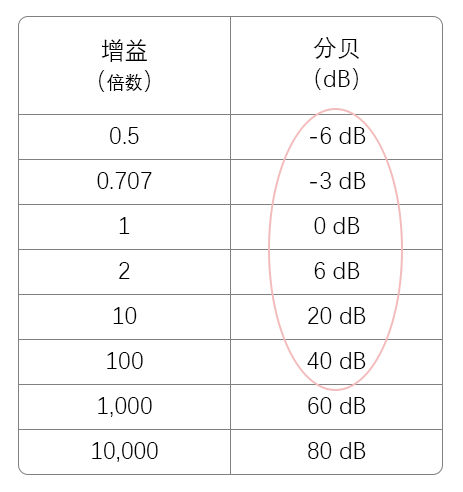
图10-1.08
其中有几个特别常见的分贝数值是我们需要记住的(图中已用红线圈出),比如:-6dB表示衰减到原来的一半、-3dB表示衰减到原来的0.707倍;6dB表示放大到原来的2倍、20dB表示放大10倍、40dB表示放大100倍。
欢迎关注本博公众号,可方便在手机端访问和索引本博技术文章:

( end of 10-1)
文章来源: 博客园
- 还没有人评论,欢迎说说您的想法!


 客服
客服


