Educational Codeforces Round 92 (Rated for Div. 2)
原作者为 DOEMsy@cnblogs, 本作品采用 CC 4.0 BY-SA 进行许可,转载请注明出处。
最近被实验室的几个项目和论文压迫得没有时间刷题,和队友一起报名的牛客和hdu多校,分别在第一场被叉姐和朝鲜人教育,感觉实力明显退步,又滚回来刷题了。
https://codeforces.com/contest/1389
A. LCM Problem
题意
给定区间 ([l,r]) ,求两个不同的数字 (x,y) ,使得 (lle xlt y le r,lle LCM(x,y) le r) 。
解题
这道题和之前的一道求区间最大 (gcd) 的签到很像,感兴趣的可以去看看 Codeforces Round #651 (Div. 2) A. Maximum GCD 。
在这个题目中的条件可以整合为 (lle x lt y le lcm le r) ,所以我们只需要让 (lcm) 最小即可 。
(x) 和 (y) 的最大公倍数最小为 (lcm_{min}(x,y) = y = 2x) ,此时令 (x = l) ,可以得到 (lcm_{min} = y = 2l) ,即为最小的答案。如果 (2l>r), 无解。
#include<bits/stdc++.h>
#define ll long long
using namespace std;
int main(){
//cin.tie(0);cout.tie(0);
//ios::sync_with_stdio(false);
//cout<<setiosflags(ios::fixed)<<setprecision(6);
//freopen("1.in", "r", stdin);
//freopen("1.out", "w", stdout);
int t;cin>>t;
while(t--){
ll l,r;cin>>l>>r;
if(2*l>r) cout<<"-1 -1"<<endl;
else cout<<l<<" "<<2*l<<endl;
}
return 0;
}
B. Array Walk
题意
给定数组 (a_1,a_2,a_3,...,a_n),起点为 (a_1) ,你可以向左向右移动,不能越界,最多 (k) 次。
并且限制不能连续的向左移动,且向左移动的次数最多为 (z) 。
每次移动到位置 (i) 可以获取分数 (a_i) ,初始分数为 (a_1) ,询问你可以得到的最大分数和。
解题
这个题在做的时候真的是一头雾水,本来以为模拟会超时,调试了半天差分(下标杀我),结果阎佬暴力过了。
这里讲下差分+数学优化的思路。
首先,向左移动不能连续,所以如果有向左移动,就只能以左右间隔的形式反复横跳。其次,以贪心的思想,最大和出现的情况,一定是只在某两个相邻位置之间反复横跳。
我们将移动分为三个阶段:
- 第一阶段,假设初始向右移动了 (i) 步,那么当前处于的位置为 (a_{i+1}) ,积分和为 (s_1 = sum_{i+1})(设 (sum_i=sum_{k=1}^i a_k),即前 (i) 项和)。
- 第二阶段,随后在 (a_{i}) 与 (a_{i+1}) 之反复横跳,设此过程中向左次数最多为 (p) ,向右次数最多为 (q) ,则 (p=min(z,lceilfrac{k-i}{2}rceil),q=min(p,k-i-p)) ,得到的积分为 (s_2 = p*a_i + q*a_{i+1})
- 第三阶段,设剩余的步数为 (k_1 = k-i-p-q) :
- 如果 (k_1>0),全部用于向右移动,可以得到的积分为 (s_3 = sum_{k_1+i+1} - sum_{i+1}) (如果有剩余步,那么第二阶段结束后位置一定在 (i+1))。
- 如果 (k_1=0),则 (s_3 = 0) ,且同时 (i+1 = k-p-q+1) ,即 (sum_{i+1} = sum_{k-p-q+1}),无论阶段二的落点是在 (i) 还是 (i+1) 。
三个阶段的总积分获取为 (res = s_1+s_2+s_3 = sum_{k-p-q+1} + p*a_i + q*a_{i+1}) 。
则最大积分和 (ans = max{res_i|res_i = sum_{k-p-q+1} + p*a_i + q*a_{i+1},iin[1,k]}) ,复杂度 (O(k))。
#include<bits/stdc++.h>
//#include<windows.h>
#define ll long long
#define fr(i,n) for(ll i=0;i<n;i++)
#define frs(i,n,flag) for(ll i=0;i<n&&flag;i++)
#define frr(i,j,n) for(ll i=j;i<n;i++)
#define r_frr(i,j,n) for(ll i=n-1;i>=j;i--)
#define frrs(i,j,n,flag) for(ll i=j;i<n&&flag;i++)
#define r_frrs(i,j,n,flag) for(ll i=n-1;i>=j&&flag;i--)
#define yes "yes"
#define no "no"
#define memset0(dp) memset(dp,0,sizeof(dp))
#define min_get(a,b) a = min(a,b)
#define max_get(a,b) a = max(a,b)
#define PI 3.14159265354
#define print_arr(begin,end) for(auto it = begin;it!=end;it++) cout<<*it<<" "; cout<<endl;
#define log_this(name,value) cout<<name<<": "<<value<<endl;
#define e5 100005
#define e6 1000006
using namespace std;
int to_int(string s) {stringstream ss;ss<<s<<endl;int a;ss>>a;return a;}
string to_str(double a) {stringstream ss;ss<<a<<endl;return ss.str();}
template<class T>inline void read(T &x){T f=1;x=0;char c=getchar();while(c<'0'||c>'9'){if(c=='-') f=-1;c=getchar();}while(c>='0'&&c<='9'){x=x*10+c-'0';c=getchar();}x*=f;}
ll a[1*e5];
ll sum[1*e5];
int main(){
//cin.tie(0);cout.tie(0);
//ios::sync_with_stdio(false);
//cout<<setiosflags(ios::fixed)<<setprecision(6);
//freopen("1.in", "r", stdin);
//freopen("1.out", "w", stdout);
int t;cin>>t;
while(t--){
ll n,k,z;cin>>n>>k>>z;
fr(i,n) cin>>a[i+1];
ll ans = 0;
sum[0] = 0;
//sum[0,i)
fr(i,n){
sum[i+1] = sum[i] + a[i+1];
}
frr(i,1,k+1){
ll p = min(1ll*z,(k+1-i)/2);
ll q = min(1ll*p,k-i-p);
ll res = sum[k-p-q+1]+p*a[i]+q*a[i+1];
ans = max(ans,res);
}
cout<<ans<<endl;
}
return 0;
}
C. Good String
题意
规定字符串 (t_1,t_2,t_3,...,t_n) 。
如果 (t_n,t_1,t_2,...t_{n-3},t_{n-2},t_{n-1}) 与 (t_2,t_3,t_4,...t_{n-1},t_n,t_1) 完全相同,则称该字符串为 Good String 。
判断给定字符串至少删除多少个字符可以变成 Good String 。
解题
简单推导可以得到 Good String 中:
- 如果 (n) 是偶数,(t_1=t_3=t_5=...=t_{n-3}=t_{n-1}) 且 (t_2 = t_4 = t_6 =...= t_{n-2} = t_n) ,如 (25252525) 。
- 如果 (n) 是奇数,(t_1=t_2=t_3=...=t_{n-1} = t_{n}) ,如 (22222)。
而且题目规定 (t_iin[0,9]) ,我们通过可以构造 (10*10) 种情况,分别算转化需要的最小花费。
复杂度 (O(10^2n)) 。
#include<bits/stdc++.h>
//#include<windows.h>
#define ll long long
#define fr(i,n) for(ll i=0;i<n;i++)
#define frs(i,n,flag) for(ll i=0;i<n&&flag;i++)
#define frr(i,j,n) for(ll i=j;i<n;i++)
#define r_frr(i,j,n) for(ll i=n-1;i>=j;i--)
#define frrs(i,j,n,flag) for(ll i=j;i<n&&flag;i++)
#define r_frrs(i,j,n,flag) for(ll i=n-1;i>=j&&flag;i--)
#define yes "yes"
#define no "no"
#define memset0(dp) memset(dp,0,sizeof(dp))
#define min_get(a,b) a = min(a,b)
#define max_get(a,b) a = max(a,b)
#define PI 3.14159265354
#define print_arr(begin,end) for(auto it = begin;it!=end;it++) cout<<*it<<" "; cout<<endl;
#define log_this(name,value) cout<<name<<": "<<value<<endl;
#define e5 100005
#define e6 1000006
using namespace std;
int to_int(string s) {stringstream ss;ss<<s<<endl;int a;ss>>a;return a;}
string to_str(double a) {stringstream ss;ss<<a<<endl;return ss.str();}
template<class T>inline void read(T &x){T f=1;x=0;char c=getchar();while(c<'0'||c>'9'){if(c=='-') f=-1;c=getchar();}while(c>='0'&&c<='9'){x=x*10+c-'0';c=getchar();}x*=f;}
int main(){
//cin.tie(0);cout.tie(0);
//ios::sync_with_stdio(false);
//cout<<setiosflags(ios::fixed)<<setprecision(6);
//freopen("1.in", "r", stdin);
//freopen("1.out", "w", stdout);
int t;cin>>t;
while(t--){
string s;cin>>s;
int a[2];
int ans = 9999999;
fr(i,10) fr(j,10){
a[0] = i,a[1] = j;
int ct = 0,k = 0;
fr(i,s.size()){
if(s[i]!=a[k&1]+'0') ct++;
else k = !k;
}
if(int(s.size()-ct)&1) if(i!=j) ct++; //只有全相等才能为奇数
ans = min(ans,ct);
//cout<<i<<" "<<j<<" "<<ans<<endl;
}
//print_arr(ct,ct+10);
cout<<ans<<endl;
}
return 0;
}
D. Segment Intersections
题意
给定两个线段数组 (a,b),初始 (a) 中所有线段等于 ([l_1,r_1]),(b) 中所有线段等于 ([l_2,r_2]) 。
每次操作可以选择两组中任意一个线段,使其长度+1。
问最少多少次操作使得 (sumlimits_{i=1}^{n}{text{intersection_length}([al_i, ar_i], [bl_i, br_i])}ge k) ,(text{intersection_length}) 表示相交长度。
解题
可以通过开销将重叠部分分为三种:
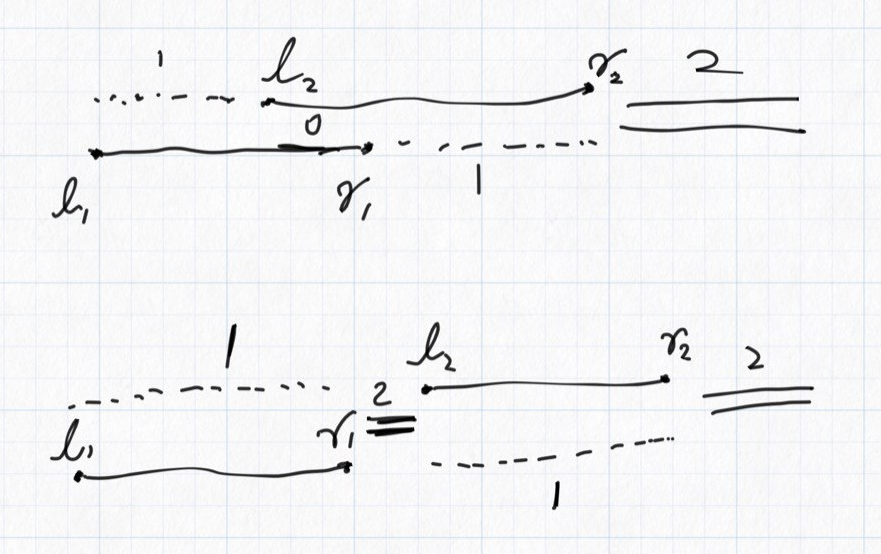
- 0 花费 原本就重叠的部分
- 1 花费 只需要延长一根线段就可以重叠的部分
- 2 花费 需要同时延长两根线段得到的重叠
你有 (n) 对一模一样的这样的线段,所以每个重叠部分最多可以计算 (n) 次。
现在就变成了一道贪心题,优先选择低开销操作,复杂度 (O(1)) 。
#include<bits/stdc++.h>
//#include<windows.h>
#define ll long long
#define fr(i,n) for(ll i=0;i<n;i++)
#define frs(i,n,flag) for(ll i=0;i<n&&flag;i++)
#define frr(i,j,n) for(ll i=j;i<n;i++)
#define r_frr(i,j,n) for(ll i=n-1;i>=j;i--)
#define frrs(i,j,n,flag) for(ll i=j;i<n&&flag;i++)
#define r_frrs(i,j,n,flag) for(ll i=n-1;i>=j&&flag;i--)
#define yes "yes"
#define no "no"
#define memset0(dp) memset(dp,0,sizeof(dp))
#define min_get(a,b) a = min(a,b)
#define max_get(a,b) a = max(a,b)
#define PI 3.14159265354
#define print_arr(begin,end) for(auto it = begin;it!=end;it++) cout<<*it<<" "; cout<<endl;
#define log_this(name,value) cout<<name<<": "<<value<<endl;
#define e5 100005
#define e6 1000006
using namespace std;
int to_int(string s) {stringstream ss;ss<<s<<endl;int a;ss>>a;return a;}
string to_str(double a) {stringstream ss;ss<<a<<endl;return ss.str();}
template<class T>inline void read(T &x){T f=1;x=0;char c=getchar();while(c<'0'||c>'9'){if(c=='-') f=-1;c=getchar();}while(c>='0'&&c<='9'){x=x*10+c-'0';c=getchar();}x*=f;}
int main(){
//cin.tie(0);cout.tie(0);
//ios::sync_with_stdio(false);
//cout<<setiosflags(ios::fixed)<<setprecision(6);
//freopen("1.in", "r", stdin);
//freopen("1.out", "w", stdout);
int t;cin>>t;
while(t--){
ll n,k;cin>>n>>k;
ll la,ra,lb,rb;
cin>>la>>ra>>lb>>rb;
ll ans = 0;
ll x0 = min(ra,rb)-max(la,lb);//原相交部分,开销为0
k -= n*max(0ll,x0);
if(k<=0){cout<<ans<<endl;continue;}
ll x1 = (max(ra,rb)-min(la,lb)-abs(x0)); //开销为1的部分
//对p根线段进行开销1操作
ll p = (x1+max(0ll,-x0))==0?n:min(n,k/(x1+max(0ll,-x0)));
k -= p*(x1+max(0ll,-x0));
ans += p*(x1+2*max(0ll,-x0));
if(k<=0){cout<<ans<<endl;continue;}
//对剩余进行补齐
ll bq = 99999999999;
if(p!=0) bq=k*2; //p=0时,没有线段相交
if(p<n) bq=min(bq,k+max(0ll,-x0)); //p=n时,没有剩余可用开销1操作
ans+=bq; //消耗补齐
cout<<ans<<endl;
}
return 0;
}
文章来源: 博客园
- 还没有人评论,欢迎说说您的想法!




 客服
客服


