推荐系统模型之 DeepFM
Preliminary
在一些推荐系统中,为了追求总点击次数最大化,会根据点击率 (click-through rate, CTR) 来排序返回给用户的商品列表;而在广告推荐的场景中,商品顺序是通过"点击率 x 单次点击收益" (CTR x bid) 来给定的。因此预测点击率,即评估用户点击某个推荐商品的可能性,在推荐系统中十分关键。
推荐系统的输入一般包括 4 部分特征:
- 用户特征 - 比如性别 (男/女),是否高消费群体,成为平台用户多久了等
- 商品特征 - 比如价格,类别等
- 用户的实时行为 - 比如登陆平台时长,商品浏览记录等
- 上下文特征 - 比如当前时间 (早上/晚上),商品的展示位置等
用户是否会点击某个推荐商品是以上 4 类特征共同作用的结果 (也许还有一些关键特征没采集到,但这并不在考虑范围内了)。而点击行为与各个特征之间往往并不是线性关系,特征之间也存在逻辑关联,这被称为特征交互 (feature interaction),即学习两个或多个原始特征之间的交叉组合 (特征交叉,feature crosses)。
此外,按照数据的连续性和离散性,特征又可分为:
- 类别特征 (categorical field)
- 连续特征 (continuous field)
其中类别特征以独热编码表示,然后与连续特征拼接,组成特征向量 (x)
其中 (x_{field_j}) 为第 (j) 个特征,由于经过了离散化处理,特征向量 (x) 表征为高维、极度稀疏。
Contribution
提出的 DeepFM 网络结构既能处理低维的特征交叉,又能处理高维的特征交叉,且不需引入特征工程,是端到端的训练。
- 低维特征交叉 (low-order feature interaction) - 两个及以下的特征交叉组合
- 高维特征交叉 (high-order feature interaction) - 两个以上的特征交叉组合
什么是端到端训练 (end2end training)?
传统的机器学习过程往往由多个独立的模块组成,被人为的分解成了若干子问题。比如图像识别问题往往通过分治将其分解为预处理,特征提取和选择,分类器设计等若干步骤。每个步骤的结果好坏会影响到下一步骤,从而影响到整个训练的效果。而在某一子问题上达到最优,也不一定能取得全局最优解。这是非端到端的。
深度学习的模型在训练过程中,从输入端喂入数据,到输出端输出预测结果,然后与真实值比较得到一个误差。这个误差会在模型中的每一层传递 (反向传播),每一层的表示都会根据这个误差来做调整,直到模型收敛或达到预期的效果才结束。整个过程可视为一个整体,这就是端到端。
而由误差理论知道,误差传播的途径本身会导致误差的累积,分为多个模块一定会导致误差累积。因此端到端训练能减少误差传播的途径,联合优化。
Methodology
DeepFM 采用了一种并行的结构,使用 FM (Factorization Machine) 学习低维的特征交叉,同时通过一个 DNN 来组合高维的特征交叉。两个组件使用相同的输入和嵌入向量。

因此 CTR 的预测值可表示为:
其中 (y_{FM}) 为 FM 部分的输出,(y_{DNN}) 为 DNN 部分的输出。这里可以加上一个偏置项 bias 来调整输出,也可不用引入这样的计算节点,因为 FM 和 DNN 两个组件中都包含了各自的 bias 项。
FM Component
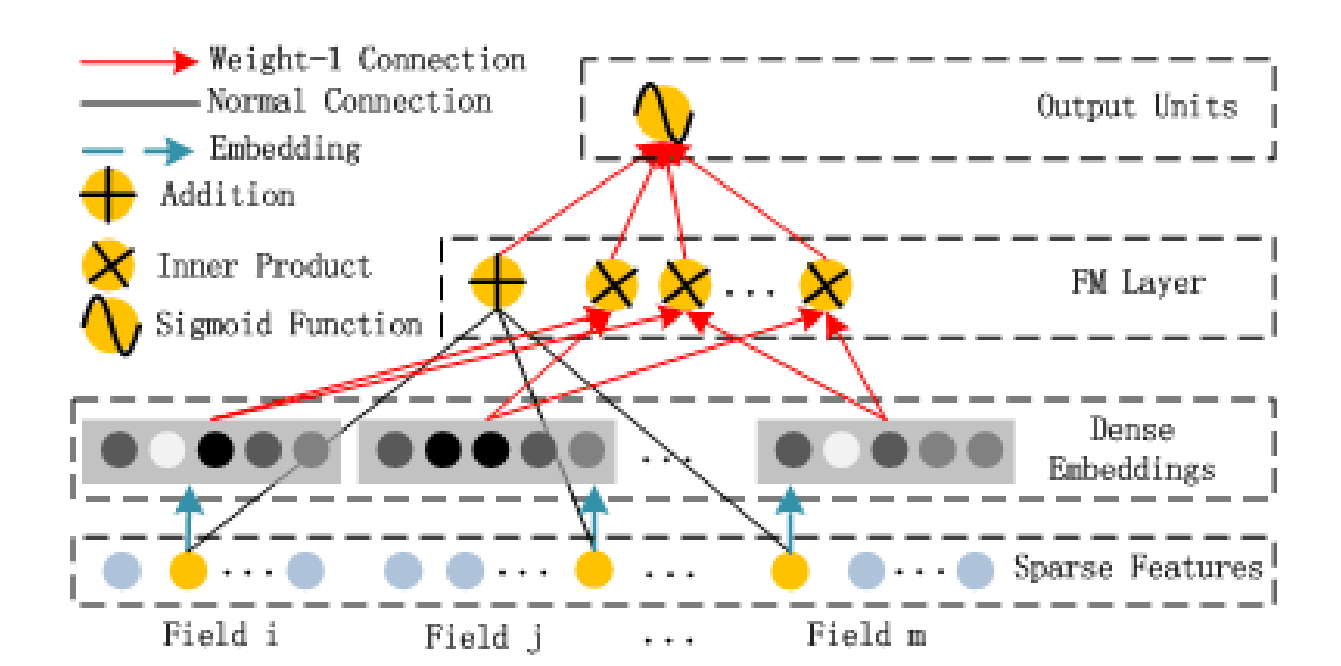
FM 组件被用来学习低维的特征交叉 (order-1 and order-2),有
其中 (w_0) 为偏置项, (X,W in mathbb{R}^{ntimes1}), (V) 为特征潜在向量 (feature latent vector) 且 (V in mathbb{R}^{ntimes k})
FM 模型原理
不同于多元线性回归模型
[hat{y} = W^T X = w_0 + sum_{i=1}^n w_i x_i ]只考虑了特征之间的线性关系 (尤其在特征向量极为稀疏的场景中刻画能力不强),
FM 对特征进行二项组合,引入新的特征,从而挖掘到了更加隐秘的信息。
[hat{y} = w_0 + sum_{i=1}^n w_i x_i + sum_{i=1}^{n} sum_{j=i+1}^n w_{i,j} x_i x_j ]其中特征参数 (w_{i,j} in mathbb{R}^{n times n}),而由于特征可能非常稀疏,比如 (n) 的取值在百万以上,这导致特征交叉后得参数数量极为庞大,需要难以计数的训练样本才能保证算法收敛。为了降低运算开销,FM 又引入了特征潜在向量 (V) 来计算特征参数:
[w_{i,j} = langle V_i, V_j rangle ]其中 (V_i, V_j in mathbb{R}^{n times k}),(k) 为超参数,不需要设置得非常大,从而大大减少了特征参数的数量。
以上算法的时间复杂度为 (O(n^2)),还可通过变形推导进一步优化至 (O(n)):
[begin{aligned} &quad sum_{i=1}^n sum_{j=i+1}^n langle V_i, V_j rangle x_i x_j \ &= frac{1}{2}Big(sum_{i=1}^n sum_{j=1}^n langle V_i, V_j rangle x_i x_j - sum_{i=1}^n langle V_i, V_i rangle x_i x_i Big)\ &= frac{1}{2}Big( sum_{i=1}^n sum_{j=1}^n sum_{f=1}^k v_{i,f} cdot v_{j,f}cdot x_i cdot x_j - sum_{i=1}^nsum_{f=1}^k v_{i,f}cdot v_{i,f} cdot x_i cdot x_i Big) \ &= frac{1}{2}sum_{f=1}^k Big (big ( sum_{i=1}^n v_{i,f}cdot x_i big) big( sum_{j=1}^n v_{j,f}cdot x_ibig) - sum_{i=1}^n v_{i,f}^2 cdot x_i^2 Big) \ &= frac{1}{2}sum_{f=1}^kBig(big( sum_{i=1}^n v_{i,f}cdot x_i big)^2 - sum_{i=1}^n v_{i,f}^2 cdot x_i^2Big) end{aligned} ]从而有:
[hat{y} = w_0 + sum_{i=1}^n w_i x_i + frac{1}{2}sum_{f=1}^kBig(big( sum_{i=1}^n v_{i,f}cdot x_i big)^2 - sum_{i=1}^n v_{i,f}^2 cdot x_i^2Big) ]这部分的实现细节:
""" https://github.com/Leavingseason/OpenLearning4DeepRecsys/deepFM.py """ # bias preds = bias # order-1 feature intreaction preds += tf.sparse_tensor_dense_matmul(_x, w_linear, name='contr_from_linear') # ... # order-2 feature interaction preds = preds + 0.5 * tf.reduce_sum(tf.pow(tf.sparse_tensor_dense_matmul(_x, w_fm), 2) - tf.sparse_tensor_dense_matmul(_xx, tf.pow(w_fm, 2)), 1, keep_dims=True)
Embedding Layer
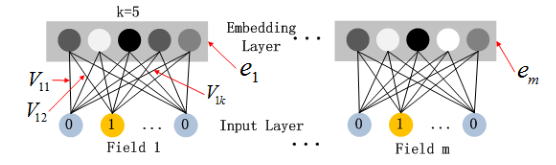
Embedding 层的作用是将高维的稀疏特征压缩成低维的稠密向量。
- 每个稀疏特征的长度不同,但它们的嵌入向量长度相同 (均为 k)
- 在 FM 组件中引入的特征潜在向量 (V) 也被用来压缩特征,作为映射时的权重向量
# feature latent vector
w_fm = tf.Variable(tf.truncated_normal([feature_cnt, dim], stddev=init_value / math.sqrt(float(dim)), mean=0), name='w_fm', dtype=tf.float32)
# ...
# embedding layer
w_fm_nn_input = tf.reshape(tf.gather(w_fm, _ind) * tf.expand_dims(_values, 1), [-1, field_cnt * dim])
如何处理连续性特征?
Deep Component
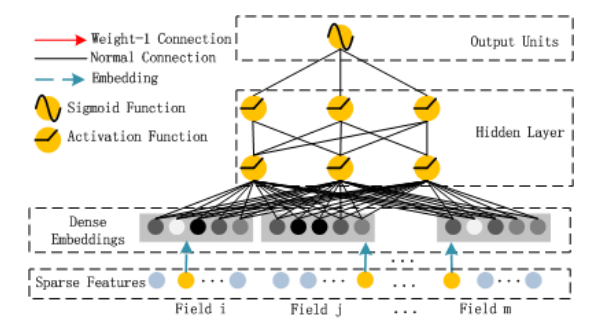
这部分是一个典型的神经网络,从代码上看,它由 2 层全连接层组成。
# y_hat = sigmoid(y_FM + y_DNN)
preds += nn_output
# ...
preds = tf.sigmoid(preds)
Reference
以下是写作中所参考的资料:
[3] 什么是端到端的训练或学习?
[4] DeepFM: A Factorization-Machine based Neural Network for CTR Prediction
[8] DeepFM: A Factorization-Machine based Neural Network for CTR Prediction, IJCAI 2017
文章来源: 博客园
- 还没有人评论,欢迎说说您的想法!




 客服
客服


