场景
- 输入一组数据,或元组,求这组数据的最小公倍数
代码实现
# -*-coding:utf-8-*-
from functools import reduce
def spread(arg):
'''解析参数,将原始参数组装成单个列表'''
ret = []
for i in arg:
if isinstance(i, list):
ret.extend(i)
else:
ret.append(i)
return ret
def lcm(*args):
numbers = []
numbers.extend(spread(list(args)))
def _gcd(x, y):
'''获取两个数的最大公约数
if not y:
return x
else:
_gcd(y,x%y)
x % y 计算两个数的余数
'''
return x if not y else _gcd(y, x % y)
def _lcm(x, y):
'''计算两个整数的最小公倍数'''
return x * y / _gcd(x, y)
return reduce(lambda x, y: _lcm(x, y), numbers)
if __name__ == "__main__":
print(lcm(12, 2))
print(lcm([1, 4, 5, 6], 8))
# 结果
12.0 # 2*6*1
120.0 # 2*4*5*3详解
- 最小公倍数: 把几个数先分别分解质因数,再把各数中的全部公有的质因数和独有的质因数提取出来连乘,所得的积就是这几个数的最小公倍数
- 分解质因数: 如下图

- 辗转相除法:辗转相除法是求两个自然数的最大公约数的一种方法,也叫欧几里德算法。
- 例如,求(319,377):
∵ 319÷377=0(余319) ∴(319,377)=(377,319); ∵ 377÷319=1(余58) ∴(377,319)=(319,58); ∵ 319÷58=5(余29) ∴ (319,58)=(58,29); ∵ 58÷29=2(余0) ∴ (58,29)= 29; ∴ (319,377)=29。 可以写成右边的格式。- 原理: 可以先求出其中任意两个数的最大公约数,再求这个最大公约数与第三个数的最大公约数,依次求下去,直到最后一个数为止。最后所得的那个最大公约数,就是所有这些数的最大公约数
- 以上算法中
_gcd(x,y)函数就是此算法, 通过 递归的方法, 指导求出两个数的最大公约数 _lcm(x,y)求得最小公倍数- reduce 内置函数得使用
扩展
- python 内置函数reduce使用:
- 格式 :
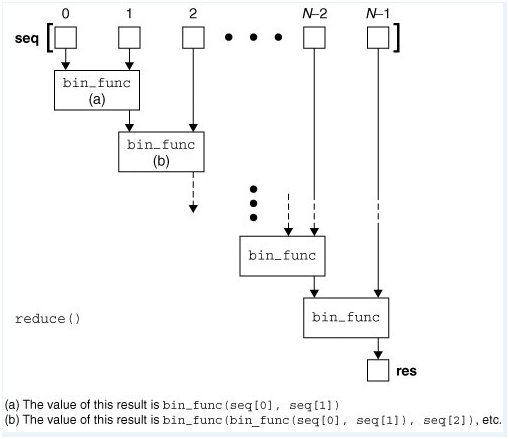
reduce (func, seq[, init()]) - 用法:
reduce()函数即为化简函数,它的执行过程为:每一次迭代,都将上一次的迭代的结果(注:第一次为init元素,如果没有指定init则为seq的第一个元素)与下一个元素一同传入func函数中去执行。在reduce()函数中,init参数是可选的,如果指定,则作为第一次迭代的第一个元素使用,如果没有指定,就取seq中的第一个元素。 - 图解:
- 应用示例 :
求一个数的阶乘
from functools import reduce def factorial(seq,n): return reduce(lambda x,y: x*y, seq,n) if __name__ == "__main__": factorial([1,2,4,7,8],8) # 结果 3548 = 8*1*2*4*7*8 - 格式 :
参考连接
- 最大公约数 : 百度百科
- python之reduce使用 : https://blog.csdn.net/SeeTheWorld518/article/details/46975857
内容来源于网络如有侵权请私信删除
- 还没有人评论,欢迎说说您的想法!




 客服
客服


