(Tarjan)算法介绍
(Tarjan)算法是用于在有向图中求强连通分量的算法
这里给出强连通分量的定义:
有向图中一个最大的图,使这个图中每个两点都能够互相到达。这个最大的图称为强连通分量,同时一个点也属于强连通分量。
据一个简单的例子,下图中的(123)也就是一个强连通分量,(4)也是一个强连通分量:
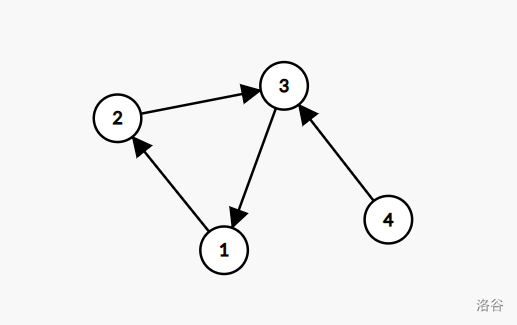
(Tarjan)算法基于(DFS),对于每一个点遍历一次,可以在(O(n))的时间复杂度求出强连通分量
(Tarjan)算法的实现
首先介绍两个数组(dfn)和(low)
他们分别表示该节点遍历到的时间和其可以遍历到的最早的祖先节点
我们发现如果一个从(u)遍历到的节点(v)的(low)比(u)的(dfn)更小,说明(v)肯定连接到了(u)的祖先节点,由此形成了一个环也就是一个强连通分量
所以我们很容易想到在遍历的过程中用子节点的(low)更新该节点的(low),接着对于同一个(low)值的点集,应该就是一个强连通分量了(类似于并查集)
但是实际上我们可以举出两种反例:
反例1
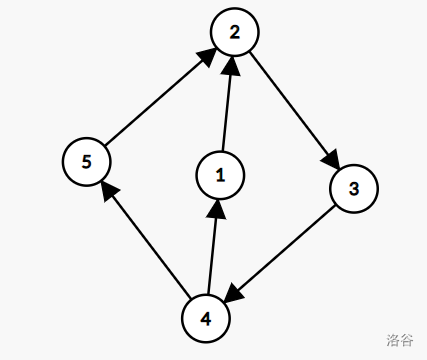
在该反例中,只有一个强连通分量,可是按上述思路却得到了两个,原因是因为节点(5)使用(2)的(low)更新时(2)的(low)还没有更新完成
反例2
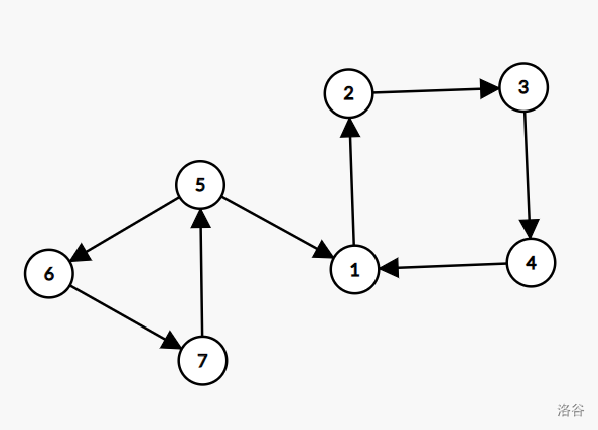
在该反例中,有两个强连通分量,可是按上述思路确只得到了一个,原因是因为,节点(5)使用了(1)的(low)进行更,可是两者并不属于同一个强连通分量
如何解决这两个问题呢?我们使用栈进行记录即可,这里不再证明使用栈的正确性(因为我不会),想了解的可以简单看看这张图


简单说说使用栈的作用,就是两个(对应上述反例):
1.遍历完成后更新整个强连通分量的(low)
2.遍历完成该强连通分量后,避免使用该强连通分量的(low)更新其他节点
有了上述解释之后,算法的过程就很好理解了
首先遍历更新
然后使用栈更新即可
割点
割点是(Tarjan)算法在无向图中的一个应用
割点的定义是对于一个双连通分量(也就是连通块),假如去掉了这个点,双连通分量就会分裂
我们考虑从一个点开始使用(Tarjan)算法进行遍历
不过这里的(Tarjan)有点不同,首先我们不需要使用栈,因为我们不需要更新一个连通块的(low),也并不需要栈来判断链接不联通的情况,因为是无向图
我们很容易发现 (我注意力又涣散了) 只有两种情况是割点
1.对于根节点,当其存在两个及以上的子节点时,他是割点
2.对于非根节点,当其子节点的(lowge dfn)时,他是割点
分别来感性证明一下
首先对于第一种情况,为什么要求是根节点,因为对于根来说,显然,所以的连通块已经遍历完成,那么此时,当他有多个子节点时,意味着,图中有多个以他作为链接的连通块,所以此时,根节点是割点。而对于非根节点,由于图还没有遍历完,所以其不存在如下性质
对于第二种情况,通俗地说,也就是当某节点的子节点链接道了他的祖先,那么他不为割点(因为形成了环),而反之则为割点,为什么要求是非根节点呢?
因为对于根节点可能存在一条链的情况,此时,他不是割点
tips:上述内容所提及的根于子节点,都是基于(Tarjan)算法的(dfs)搜索树
接着是代码实现:
#include<bits/stdc++.h>
#define ll long long
#define ull unsigned long long
using namespace std;
const int N=2e4+10;
int n,m;
int u,v;
vector<int>edge[N];
int low[N];
int dfn[N];
bool g[N];
int deep;
int num;
void dfs(int x,int fa)
{
int child=0;
deep++;
low[x]=deep;
dfn[x]=deep;
for(int i=0;i<edge[x].size();i++)
{
int next=edge[x][i];
if(dfn[next]==0)
{
if(x==fa)
child++;
dfs(next,x);
low[x]=min(low[x],low[next]);
if(x!=fa&&low[next]>=dfn[x])
{
g[x]=true;
}
}
else
{
low[x]=min(low[x],dfn[next]);
}
}
if(child>=2)
{
g[x]=true;
}
return;
}
int main()
{
std::ios::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
cin>>n>>m;
for(int i=1;i<=m;i++)
{
cin>>u>>v;
edge[u].push_back(v);
edge[v].push_back(u);
}
for(int i=1;i<=n;i++)
{
if(dfn[i]==0)
{
dfs(i,i);
}
}
for(int i=1;i<=n;i++)
{
if(g[i]==true)
{
num++;
}
}
cout<<num<<endl;
for(int i=1;i<=n;i++)
{
if(g[i]==true)
{
cout<<i<<" ";
}
}
return 0;
}
缩点
缩点是基于(Tarjan)实现的一种算法,他的目的是,将有向图中的强连通分量缩成一个点,从而使原图变成一个有向图无环图,来满足拓扑排序等算法的使用需要
因为思想较为简单所以直接放上模板题的代码(缩点+拓扑排序+(DP))
#include<bits/stdc++.h>
#define ll long long
#define ull unsigned long long
using namespace std;
int n,m;
int u[100001],v[100001];
int l;
int a[10001];
int sum[10001];
bool f[10001];
int z[10001];
int low[10001];
int dfn[10001];
bool vis[10001];
vector<int>edge[10001];
int r[10001];
vector<int>e[10001];//top边
vector<int>ne[10001];//单向边
int dp[10001];
int ans;
int deep;
queue<int>q;
void dfs(int x)
{
deep++;
dfn[x]=deep;
low[x]=deep;
z[++l]=x;
vis[x]=true;
for(int i=0;i<edge[x].size();i++)
{
int next=edge[x][i];
if(dfn[edge[x][i]]==0)
{
dfs(next);
low[x]=min(low[x],low[next]);
}
else
{
if(vis[next]==true)
{
low[x]=min(low[x],low[next]);
}
}
}
if(dfn[x]==low[x])
{
while(z[l]!=x)
{
low[z[l]]=dfn[x];
vis[z[l]]=false;
l--;
}
vis[z[l]]=false;
l--;
}
return;
}
void top()
{
for(int i=1;i<=n;i++)
{
if(f[i]==true&&r[i]==0)
{
q.push(i);
r[i]=-1;
}
}
while(!q.empty())
{
int x=q.front();
q.pop();
for(int i=0;i<e[x].size();i++)
{
r[e[x][i]]--;
if(r[e[x][i]]==0)
{
q.push(e[x][i]);
r[e[x][i]]=-1;
}
}
int maxs=0;
for(int i=0;i<ne[x].size();i++)//拓扑排序的过程中DP
{
maxs=max(maxs,dp[ne[x][i]]);
}
dp[x]=sum[x]+maxs;
ans=max(ans,dp[x]);
}
return;
}
int main()
{
std::ios::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
cin>>n>>m;
for(int i=1;i<=n;i++)
{
cin>>a[i];
}
for(int i=1;i<=m;i++)
{
cin>>u[i]>>v[i];
edge[u[i]].push_back(v[i]);
}
for(int i=1;i<=n;i++)
{
if(dfn[i]==0)
{
dfs(i);
}
}
for(int i=1;i<=n;i++)//其实low就可以看作是强连通分量的一个祖先(跟并查集一样)
{
sum[low[i]]+=a[i];//每个强连通分量的点数
f[low[i]]=true;//缩成的点
}
for(int i=1;i<=m;i++)
{
u[i]=low[u[i]];
v[i]=low[v[i]];
if(u[i]!=v[i])//自环不能连边
{
r[u[i]]++;
e[v[i]].push_back(u[i]);
ne[u[i]].push_back(v[i]);
}
}
top();
cout<<ans;
return 0;
}
2-sat
2-sat是(Tarjan)算法延申出的一个问题
其旨在解决形如
这样的问题是否有解以及构造解
解决的方法非常的简单,就是在含义如(x1=1)和(x2=0)之间连一条有向边,表示我应该由(x1=1)的状态得出(x2=0)的状态
tips,这里有一些常见的问题,例如连接(x1=1)到(x1=0)表示的什么含义,其实就是表示若(x1=1)应该变成(x1=0)即(x1ne1),(x1=0)
然后跑(Tarjan),当(x=1)和(x=0)出现在同一强连通分量时,意味着出现了(x=1)要变为(x=0)并且(x=0)要变为(x=1),出现矛盾,无解
反之有解
至于构造,显然在(x=0)和(x=1)中,我们应该选择拓扑序更大的,因为显然连接某状态的边更多说明更多状态会推导出该状态,所以会更优
这里附上模板题及代码
P4782 【模板】2-SAT 问题
#include<bits/stdc++.h>
#define ll long long
#define ull unsigned long long
using namespace std;
const int N=1e6+10;
const int M=1e6+10;
int n,m;
int a,op1,b,op2;
vector<int>edge[N*2];//0 1
int deep;
int dfn[N*2];
int low[N*2];
int z[N*2];
int l;
bool vis[N*2];
int color[N*2];
int colnum;
void dfs(int x)
{
deep++;
l++;
z[l]=x;
low[x]=deep;
dfn[x]=deep;
vis[x]=true;
for(int i=0;i<edge[x].size();i++)
{
int next=edge[x][i];
if(dfn[next]==0)
{
dfs(next);
low[x]=min(low[x],low[next]);
}
else
{
if(vis[next]==true)
{
low[x]=min(low[x],low[next]);
}
}
}
if(dfn[x]==low[x])
{
colnum++;
while(z[l]!=x)
{
low[z[l]]=low[x];
vis[z[l]]=false;
color[z[l]]=colnum;
l--;
}
vis[z[l]]=false;
color[z[l]]=colnum;
l--;
}
return;
}
int main()
{
std::ios::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
cin>>n>>m;
for(int i=1;i<=m;i++)
{
cin>>a>>op1>>b>>op2;
if(op1==0)
{
if(op2==0)
{
edge[a+n].push_back(b);
edge[b+n].push_back(a);
}
else
{
edge[a+n].push_back(b+n);
edge[b].push_back(a);
}
}
else
{
if(op2==0)
{
edge[a].push_back(b);
edge[b+n].push_back(a+n);
}
else
{
edge[a].push_back(b+n);
edge[b].push_back(a+n);
}
}
}
for(int i=1;i<=n*2;i++)
{
if(dfn[i]==0)
{
dfs(i);
}
}
for(int i=1;i<=n;i++)
{
if(low[i]==low[i+n])
{
cout<<"IMPOSSIBLE";
return 0;
}
}
cout<<"POSSIBLE"<<endl;
for(int i=1;i<=n;i++)
{
if(color[i]<color[i+n])
cout<<0<<" ";
else
cout<<1<<" ";
}
return 0;
}
这里存在一个细节,强连通分量的编号越小,说明拓扑序越大。
其实这也比较好理解
举一个例子

图中红蓝两个强连通分量,显然蓝的编号更小,拓扑序越大,因为显然如果一个强连通分量对于别的强连通分量有连边,(Tarjan)算法会先遍历另外一个强连通分量,然后再对改强连通分量进行更新。
所以先更新的那个强连通分量满足以下两个条件
1.出边少
2.入边多
即拓扑序大,更优
前缀后缀优化点集内建边
这个由于我太菜了,并没有搞懂,所以直接背了 (刚刚逝了逝,发现已经忘了)
提供一篇很好的博客和例题
文章来源: 博客园
- 还没有人评论,欢迎说说您的想法!




 客服
客服


