习题7.1

感知机的对偶形式与支持向量机的对偶形式的区别在于：感知机是通过假设参数变化的增量进行转换；而支持向量机是通过求解带约束的最优化问题，通过拉格朗日对偶性转为无约束最优化问题去求解。

感知机的原始形式

最优化目标函数： (mathop{min} limits_{w,b} L(w,b) = - sum y_i(w*x_i+b))

感知机的对偶形式

最优化目标函数： (mathop{min} limits_{alpha , b} L(alpha , b) = - sum y_i(sum limits_{j=1}^N alpha_j y_j x_j * x_i +b))

支持向量机的原始形式

最优化目标函数： (mathop{min} limits_w frac{1}{2} left| w right|^2)

约束条件： (y_i(w*x_i+b)=1 ge 0)

支持向量机的对偶形式

最优化目标函数： (mathop{min} limits_{alpha} frac{1}{2} sum limits_i sum limits_j alpha_i alpha_j y_i y_j (x_i*x_j) - sum limits_i alpha_i)

约束条件：(sum limits_i alpha_iy_i=0) ， (alpha_i ge 0)

习题7.2

通过计算可得

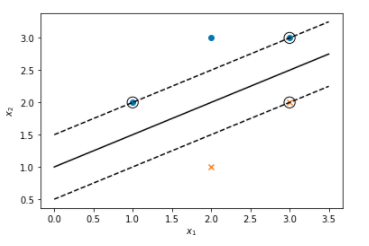
最大间隔分离超平面： (-x_1 +2x_2-2=0)

分类决策函数： (f(x) = sign(-x_1 +2x_2-2))

支持向量： (x^{(1)} = (1,2)^T, x^{(3)} = (3,3)^T, x^{(5)} = (3,2)^T)

具体结果如图所示

习题7.3

根据原始形式，构造拉格朗日函数

(L(w,b,xi, alpha, mu) = frac{1}{2} left| w right|^2 + C sum xi_i^2 - sum alpha_i(y_i(w*x_i+b)-1+xi_i) - sum mu_ixi_i)

对 (w,b,xi) 进行求偏导，解满足KKT条件。

(frac{partial L}{partial w} = w - sum alpha_iy_ix_i = 0) ， (frac{partial L}{partial b} = - sum alpha_iy_i = 0) ，(frac{partial L}{partial xi_i} =2Cxi_i - mu_i - alpha_i = 0) ，(alpha_i(y_i(w*x_i+b)-1+xi_i)=0) ， (mu_ixi_i=0) ，(y_i(w*x_i+b)-1+xi_i ge 0) ， (xi_i ge 0) ，(alpha_i ge 0) ， (mu_i ge 0)

所以可得

(w = sum alpha_iy_ix_i)， (sum alpha_iy_i = 0) ，(xi_i = frac{mu_i+alpha_i}{2C})

代入到拉格朗日函数，可得

(L(alpha, mu) = -frac{1}{2} sum sum alpha_ialpha_jy_iy_j(x_i*x_j) +sum alpha_i -frac{1}{4C} sum (mu_i + alpha_i)^2)

对拉格朗日函数求极大，并将问题进行转化

最优化目标函数： (mathop{max} limits_{alpha, mu} -frac{1}{2} sum limits_i sum limits_j alpha_i alpha_j y_i y_j (x_i*x_j) + sum limits_i alpha_i - frac{1}{4C} sum limits_i (mu_i+alpha_i)^2)

约束条件：(sum limits_i alpha_iy_i=0) ， (alpha_i ge 0) ， (mu_i ge 0) ，(frac{mu_i + alpha_i}{2C} ge 0) ， (mu_i* frac{mu_i+alpha_i}{2C} =0)

习题7.4

根据定义7.7，若对任意的 (x^{(1)}, x^{(2)}, ..., x^{(m)}) ， (K(x^{(i)}, x^{(j)})) 对应的 Gram矩阵为半正定矩阵时， (K(x,z)) 为正定核。

所以

(sum limits_{i,j} c_i c_j K(x^{(i)}, j^{(j)}) = sum limits_{i, j} c_i c_j (x^{(i)}*x^{(j)})^p = (sum limits_i c_ix^{(i)})(sum limits_j c_jx^{(j)})(x^{(i)}*x^{(j)})^{p-1} = left| sum limits_i c_i x^{(i)} right|^2 (x^{(i)}*x^{(j)})^{p-1})

因为 (p) 是正整数， 所以 (p-1 ge 0)

所以 (sum limits_{i,j} c_i c_j K(x^{(i)}, j^{(j)}) ge 0) ，Gram矩阵为半正定矩阵， (K(x,z)) 为正定核。

• 还没有人评论，欢迎说说您的想法！

相关课程

基于 OpenVINO™ 的 AI 视觉应用基础课

56020 0元 限免

英特尔® OpenVINO™工具套件初级课程

293021 0元 限免

基于 OpenVINO™ 的 AI 视觉应用进阶课

42027 0元 限免