前言
数据结构可划分为线性结构、树型结构和图型结构三大类。前面几篇讨论了数组、栈和队列、链表都是线性结构。树型结构中每个结点只允许有一个直接前驱结点,但允许有一个以上直接后驱结点。树型结构有树和二叉树(Binary Tree)两种,二叉树最多只允许有两个直接后继结点的有序树。
本篇将学习树的用途、运行机制以及创建树的方法。
为什么使用二叉树
Q: 为什么要用到树?
A: 因为它通常结合了另外两种数据结构的优点:1)有序数组 2)链表。在树中查找数据项的速度和在有序数组中查找一样快,并且插入数据项和删除数据项的速度也和链表一样
A: 在有序数组中插入数据项太慢,我们知道在有序数组里二分查找的时间复杂度为O(log2N),然而要插入一个新数据项,就必须首先查找新数据项插入的位置,然后把所有比新数据项大的都往后移动一位,以便给新数据项腾出空间。这样多次地移动很费时,平均来讲要移动数组一半的数据项(N/2次移动)。同理删除操作也一样慢。显而易见,如果要做很多地插入和删除操作,就不该选用有序数组。
A: 在链表查找太慢,查找必须从头开始,依次访问链表中的每一个数据项,直到找到该数据项为止。因此平均需要访问N/2个数据项,把每个数据项的值和要找的数据项做比较,这个过程很慢,费时O(N)。不难想到可以通过有序链表来加快查找速度,但这样做是没有用的,即使是有序链表也必须是从头开始依次访问数据项,因为链表中不能直接访问数据项,必须通过数据项的链式引用才可以。
Q: 树是什么?
A: 树是有边连接的结点而构成,下图显示了一棵树,用圆代表结点,连接圆的直线代表边。 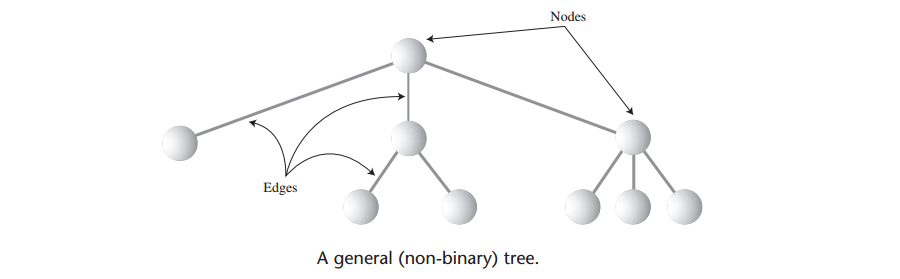
A: 人们把树作为抽象的数学实体来广泛地研究,因此有大量的关于树的理论知识。其实树是范畴更广的图的特例。
A: 树是由n(n≥0)个结点构成的集合。n = 0的树为空树;对n > 0的树T有:
1) 有一个特殊的结点称为根结点,根结点没有前驱结点;
2) 当n > 1时,除根结点外其他结点被分成m(m>0)个互不相交的集合T1, T2, ……, Tm,其中每一个集合Ti(0≤i≤m)本身又是一棵同类的子树。
显然树是递归定义的,因此,在树的算法中频繁地出现递归。
A: 本篇讨论的是一种特殊的树-二叉树。二叉树的每个结点最多有两个子结点。
结点的子结点可以多于两个,这种树称为多路树,关于多路树请参阅另两篇:
什么是2-3-4树
外部存储
Q: 树的术语?
下图展示了很多用于二叉树的一些树的术语。 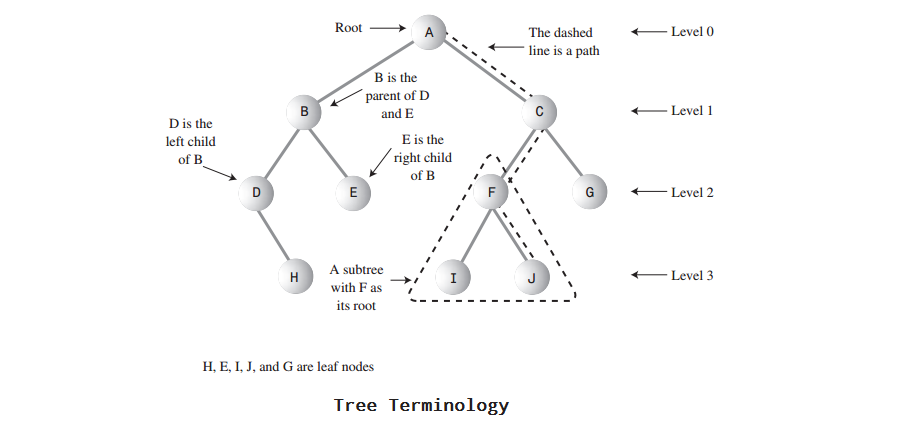
路径: 设想一下顺着连接结点的边从一个结点走到另一个结点,所经过的结点的顺序排列就被称为“路径”。显然可以看出,从根到其他任何一个结点都必须只有一条(且只有一条)路径,否则就不是树,如下图(A non-tree)它违反了这条规则。 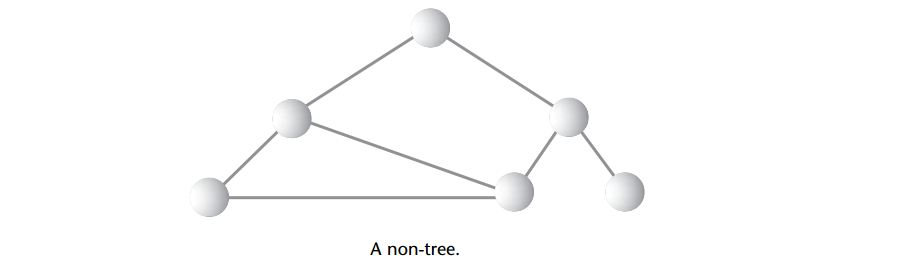
结点: 结点由数据元素和构造数据元素之间的关系的指针组成
结点的度: 结点所拥有子树的个数被称为该结点的度
叶结点: 度为0的结点被称为叶结点(也称为终端结点),如上图(Tree Terminology)H, E, I, J, G均为叶结点
分支结点: 度不为0的结点称为分支结点(也称为非终端结点)。显然一棵树中除了叶结点外所有结点都是分支结点
根结点: 树顶端的结点称为“根结点”。一棵树只有一个根
子结点: 树中一个结点的子树的根结点称作这个结点的子结点,如上图(Tree Terminology)结点B,C是结点A的子结点。子结点也被称作后继结点
父结点: 若树中某结点有子结点,则这个结点就称作它的子结点的父结点。如上图(Tree Terminology)结点A是结点B,C的父结点。父结点也称为直接前驱结点
兄弟结点: 具有相同的父结点的结点称为兄弟结点(sibling node),如上图(Tree Terminology)结点B,C具有相同的父结点A,所以称结点B,C为兄弟结点
树的度: 树中所有结点的度的最大值称为该树的度
结点的层次: 从根结点到树中某结点所经路径上的分支数称为该结点的层次。根结点层次规定为0,这样其他结点的层次就是它的父结点的层次加1
树的深度: 树中所有结点的层次的最大值被称为该树的深度
访问: 当程序控制流程到达某个结点时,被称为“访问”该结点,通常是为了在这个结点处执行某种操作,例如查看结点某个数据字段的值或显示结点。如果仅仅是在路径上从某个结点到另一个结点时经过了一个结点,不认为是访问了这个结点。
关键字: 可以看到,对象中通常会有一个数据域被指定为关键字值。在树的图形中,如果用圆表示保存数据项的结点,那么一般将这个数据项值显示在这个圆中
二叉搜索树
Q: 什么是二叉搜索树?
A: 我们要学习的二叉树在学术上称为二叉搜索树,二叉搜索树(binary search tree)的特征:一个结点的左子结点的关键字值小于这个结点,右子结点的关键字值大于或等于这个父结点。下图显示了一棵二叉搜索树。 
A: 二叉搜索树是两种库集合类TreeSet和TreeMap实现的基础
Q: 什么是满二叉树、完全二叉树?
A: 在一棵二叉树中,如果所有分支结点都存在左子树和右子树,并且所有叶子节点都在同一层上,这样的二叉树被称作满二叉树。 
A: 如果一棵具有n个结点的二叉树的结构与满二叉树的前n个结点的结构相同,这样的二叉树称作完全二叉树。
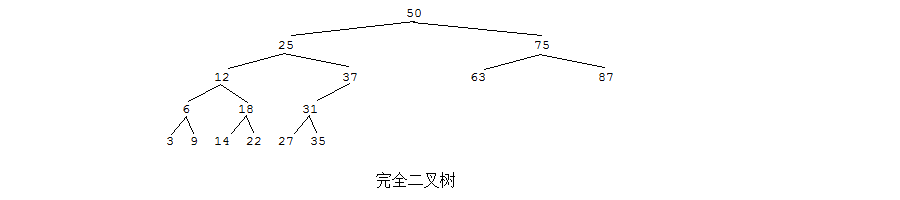
A: 显然,满二叉树一定是完全二叉树
Q: 二叉树的存储结构有哪些?
A: 顺序存储结构和链式存储结构。本篇先介绍链式存储结构,然后再介绍顺序存储结构
二叉树的链式存储结构
Q: 如何用java代码表示树?
A: 二叉树的链式存储结构是用指针建立二叉树中结点之间的关系。
A: 二叉树最常用的的链式存储结构是二叉链。二叉链存储结构的每个结点包含三个域,分别是数据域data、左孩子指针域leftChild和右孩子指针域rightChild。二叉链存储结构中每个结点的图示结构为: 
二叉树的链式存储结构如下: 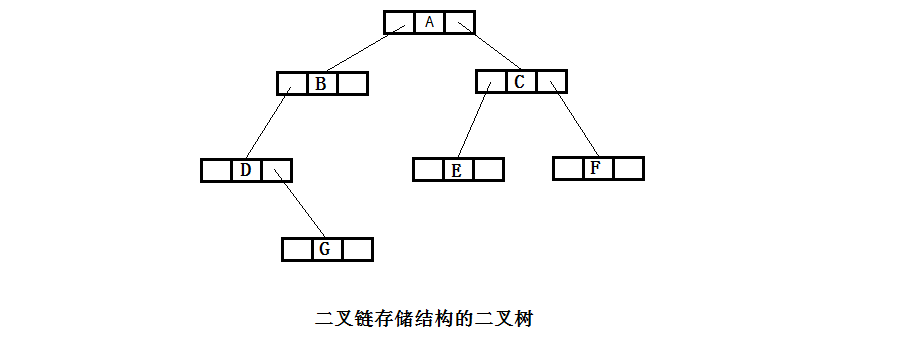
A: 相关类设计包括Node类和Tree类
Node类如下:
class Node {
public int mKey;
public double mData;
public Node mLeftChild;
public Node mRightChild;
public void displayNode() {
}
}
Tree类如下:
class Tree {
private Node mRoot;
public Node find(int key) {}
public void insert(int key, double data) {}
public boolean delete(int key) {}
public void displayTree() {}
// various other methods
}
下面将逐个介绍树的操作
查找结点
Q: 如何用Java代码实现?
A: 根据关键值查找结点是树里面最简单的操作,如下图是查找结点57的示意图 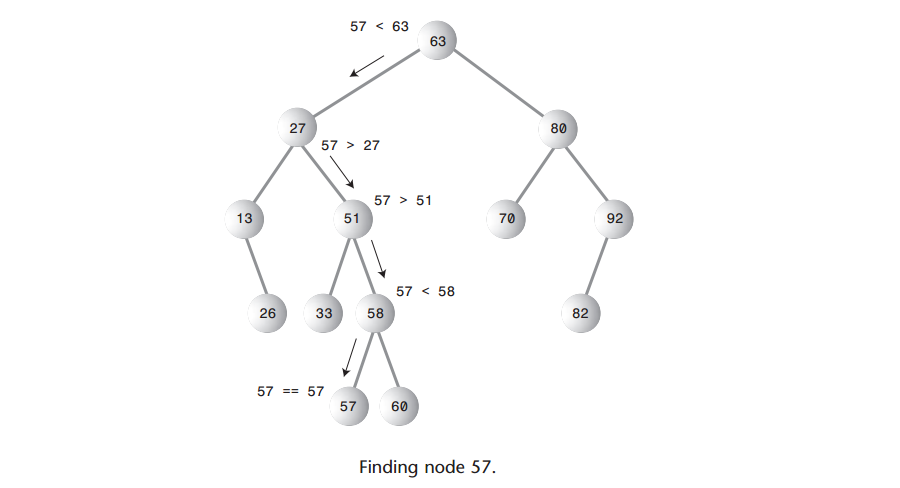
A: 下面是find()的代码,这个过程用变量current来保存正在查看的结点。
public Node find(int key) {
// assumes non-empty tree
Node current = mRoot; // start at root
while (current.mKey != key) { // while not match,
if (key < current.mKey) { // go left?
current = current.mLeftChild;
} else { // or go right?
current = current.mRightChild;
}
if (current == null) {
return null; // didn't find it
}
}
return current; // found it
}
Q: 效率如何?
A: 查找结点的时间取决于这个结点所在的层数,它的时间复杂度为O(log2N)
插入一个结点
Q: 如何用Java代码实现?
A: 要插入结点,必须先找到插入的地方。从根开始查找有一个相应的结点,它将是新结点的父结点。当父结点找到了,新的结点就可以连接到它的左子结点或右子结点,这取决于新结点的值比父结点的值大还是小。如下图: 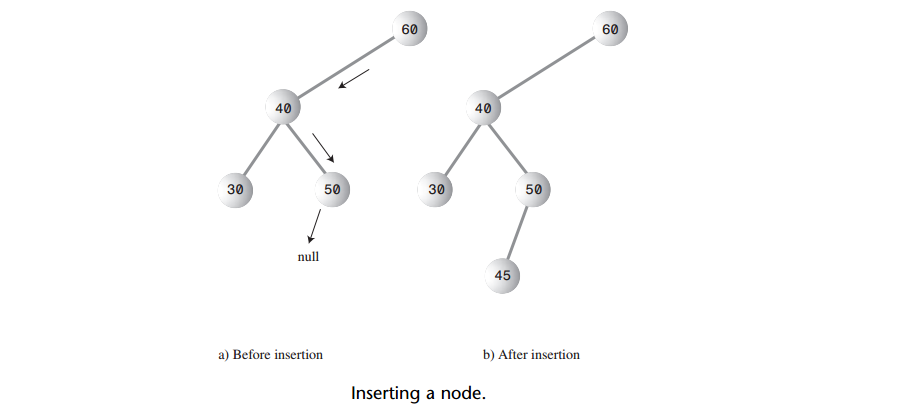
A: 插入结点的位置总会被找到的(除非存储器溢出),找到后,新结点接到树上,while循环从return调出。
下面是insert()的代码:
public void insert(int key, double data) {
Node node = new Node(); // make new node
node.mKey = key;
node.mData = data;
if (null == mRoot) { // no node in root
mRoot = node;
} else { // root occupied
Node current = mRoot; // start at root
Node parent = null;
while (true) { // exits internally(出口在内部)
parent = current;
if (key < current.mKey) { // go left?
current = current.mLeftChild;
if (null == current) {
parent.mLeftChild = node;
return;
}
} else { // or go right?
current = current.mRightChild;
if (null == current) {
parent.mRightChild = node;
return;
}
}
}
}
}
A: 这里用一个新的变量parent(current的父结点),来存储遇到的最后一个不是null的结点,必须这样做,因为current在查找的过程中会变成null,才能发现它查找过的上一个结点没有对应的子结点。如果不存储parent,就会失去插入新结点的位置。
二叉树遍历
Q: 遍历有哪些基本方法?
A: 从二叉树的定义可知,一棵二叉树由三部分组成:根结点、左子树和右子树。若规定D、L、R分别代表“访问根结点”、“遍历根结点的左子树”、“遍历根结点的右子树”,则共有6种组合:LDR, DLR, LRD, RDL, DRL, RLD。由于先遍历左子树和先遍历右子树在算法设计上没有本质区别,所以这里只讨论6种组合的前3种:DLR,LDR, LRD。根据遍历算法对访问根结点处理的位置,称这3种遍历算法分别为前序遍历(DLR)、中序遍历(LDR)和后序遍历(LRD)。
A: 二叉搜索树最常用的遍历方法是中序遍历,所以先来看看中序遍历,再简单学习其他两种遍历方法。 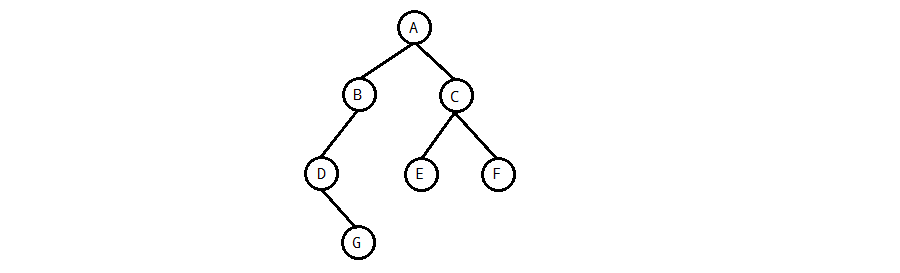
Q: 中序遍历(Inorder Traversal)的算法?
A: 中序遍历(LDR)的递归算法为:
若二叉树为空,则算法结束,否则
1) 中序遍历根结点的左子树;
2) 访问根结点;
3) 中序遍历根结点的右子树
如上图所示的二叉树,中序遍历访问的结点的次序为:D、G、B、A、E、C、F
Q: 前序遍历(Preorder Traversal)的算法?
A: 前序遍历(DLR)递归算法为:
若二叉树为空,则算法结束,否则
1) 访问根结点
2) 前序遍历根结点的左子树
3) 前序遍历根结点的右子树
如上图所示的二叉树,中序遍历访问的结点的次序为:A、B、D、G、C、E、F
Q: 后序遍历(Postorder Traversal)的算法?
A: 后序遍历(LRD)递归算法为:
若二叉树为空,则算法结束,否则:
1) 后序遍历根结点的左子树
2) 后序遍历根结点的右子树
3) 访问根结点
如上图所示的二叉树,中序遍历访问的结点的次序为:G、D、B、E、F、C、A
Q: 层次遍历的算法?
A: 除了上面所说的三种遍历算法外,二叉树还有层次遍历,不过该遍历不是很常用。
A: 层次遍历的要求是:自上而下,同一层中自左至右,逐层访问树的结点的过程就是层序遍历
A: 如上图所示的二叉树,层次遍历访问的结点的次序为:A、B、C、D、E、F、G
Q: 注意事项?
A: 虽然二叉树是一种非线性结构,二叉树不能像单链表那样每个结点都有一个唯一的前驱结点和唯一的后继结点,但对于二叉树用一种特定的遍历方法来遍历时,其遍历序列一定是线性的,且是唯一的。
A: 如下图的两棵树的前序遍历序列是相同的,但它们是两颗不同的二叉树。因此一个二叉树的遍历序列不能决定一棵二叉树的结构 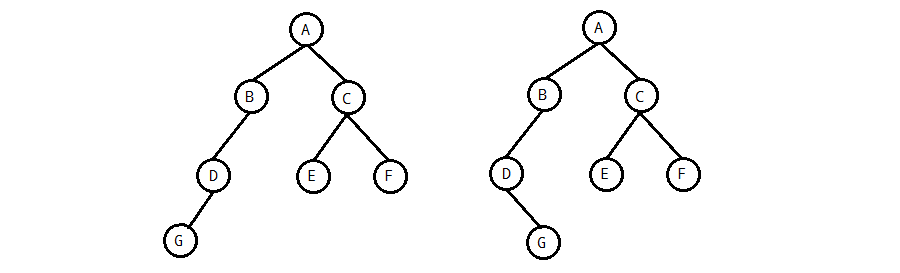
A: 某些不同的遍历序列组合可以唯一确定一棵二叉树。可以证明,给定一棵二叉树的前序序列和中序序列,则可以唯一确定一棵二叉树的结构。
查找最大值和最小值
Q: 如何查找?
A: 在二叉搜索树中得到最大值和最小值是轻而易举的事情。要找到最小值,先走到根的左子结点处,然后接着走到子结点的左子结点,以此类推,直到找到一个没有左子结点的结点,该结点就是最小值的结点,如下图所示:
/**
* 获取最小值对应的节点
*/
public Node getMininum() {
Node current = mRoot;
Node last = null;
while (current != null) { // start at root until the bottem
last = current; // remember node
current = current.mLeftChild; // go left child
}
return last;
}
A: 同理查找最大值
删除结点
Q: 删除结点会遇到哪些场景?
A: 删除结点是二叉搜索树里最复杂的操作,但是,删除结点在很多树中的应用又非常重要,所以要详细研究并总结其特点。
A: 删除结点要从查找要删的结点开始入手,方法与前面的find()和insert()相同。找到结点后,这个要删除的结点可能会有三种情况需要考虑:
1) 该结点是叶结点
2) 该结点有一个子结点
3) 该结点有两个子结点
Q: 如何删除叶结点?
A: 要删除叶结点,只需要把该结点的父结点的对应成员指针设为null即可。要删除的结点依然存在,只是它已经不是树的一部分了。如下图: 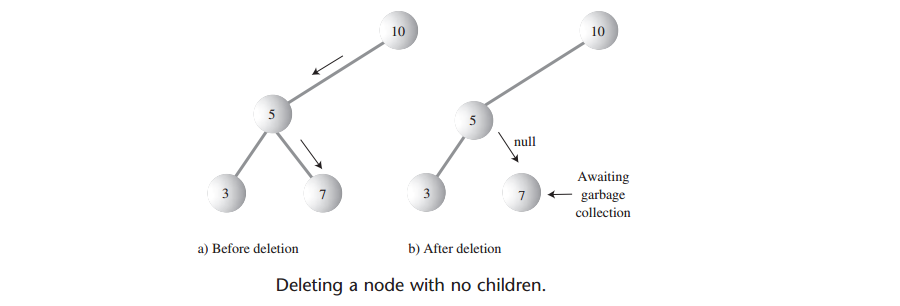
A: delete()的第一部分和find()、insert()方法很像,先要找到删除的结点。和insert()一样,需要保存要删除结点的父结点,这样就可以修改它的对应成员指针了。如果找到结点了,就从while循环跳出,parent的对应成员指针保存要删除结点。如果找不到删除的结点,就从delete()方法返回false。
public boolean delete(int key) {
Node current = mRoot;
Node parent = null;
boolean isLeftChild = false;
while (current.mKey != key) { // search for node
parent = current;
if (key < current.mKey) { // go left?
current = current.mLeftChild;
isLeftChild = true;
} else { // go right?
current = current.mRightChild;
isLeftChild = false;
}
if (current == null) { // didn't find it
return false;
}
}
// found nodes to delete
// continues ...
}
A: 找到结点后,先要检查它是不是真的没有子结点。如果它没有子结点,还需要检查它是不是根。如果它是根的话,只需要把它设为null,这样就清空了整棵树,否则就把它的父结点的leftChild或者rightChild的指针设为null,断开父结点和那个要删除结点的连接。
// delete() continued ...
// if no childrent, simply delete it
if (current.mLeftChild == null && current.mRightChild == null) {
if (current == mRoot) {
mRoot = null;
} else if (isLeftChild) {
parent.mLeftChild = null;
} else {
parent.mRightChild = null;
}
// continues ...
Q: 如何删除有一个子结点的结点?
A: 这个结点只有两个连接:连向父结点和连向它唯一的子节点。需要从这个序列中“剪断”这个结点,把它的子结点直接连接到它的父结点。如下图所示: 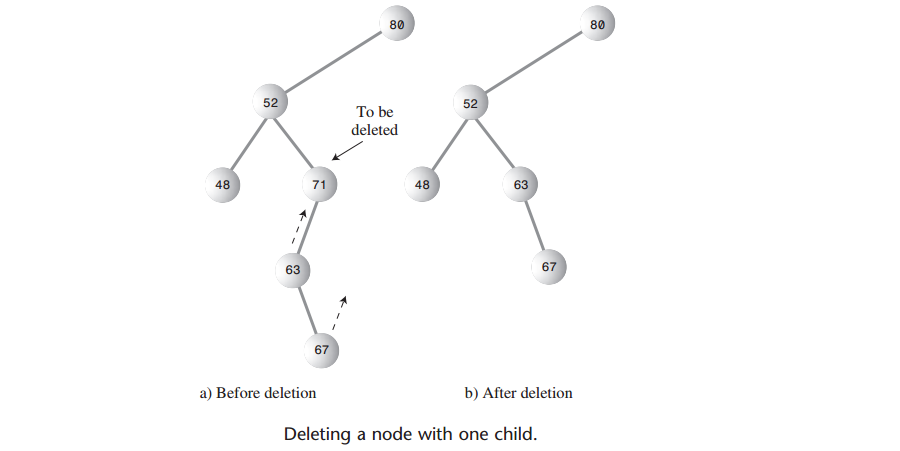
A: 有四种不同情况:
1)要删除的结点的子结点是左边的,同时是父节点的左子树; 
2)要删除的结点的子节点是右边的,同时是父节点的左子树; 
3)要删除的结点的子结点是左边的,同时是父节点的右子树;
4)要删除的结点的子节点是右边的,同时是父节点的右子树;
还有一个特殊的情况:被删除的结点可能是根,它没有父节点,只是被合适的子树所代替。下面是相关代码:
// delete() continued ...
// if no right child, replace with left subtree
} else if (current.mRightChild == null) {
if (current == mRoot) {
mRoot = mRoot.mLeftChild;
} else if (isLeftChild) { // left child of parent
parent.mLeftChild = current.mLeftChild;
} else { // right child of parent
parent.mRightChild = current.mLeftChild;
}
// if no left child, replace with right subtree
} else if (current.mLeftChild == null) {
if (current == mRoot) {
mRoot = mRoot.mRightChild;
} else if (isLeftChild) { // left child of parent
parent.mLeftChild = current.mRightChild;
} else { // right child of parent
parent.mRightChild = current.mRightChild;
}
// continued ...
Q: 如何删除有两个子结点的结点?
A: 如果要删除的结点有两个子结点,就不能只是用它的一个子结点代替它,为什么不能这样呢?如下图,要删除结点25就是一个问题。 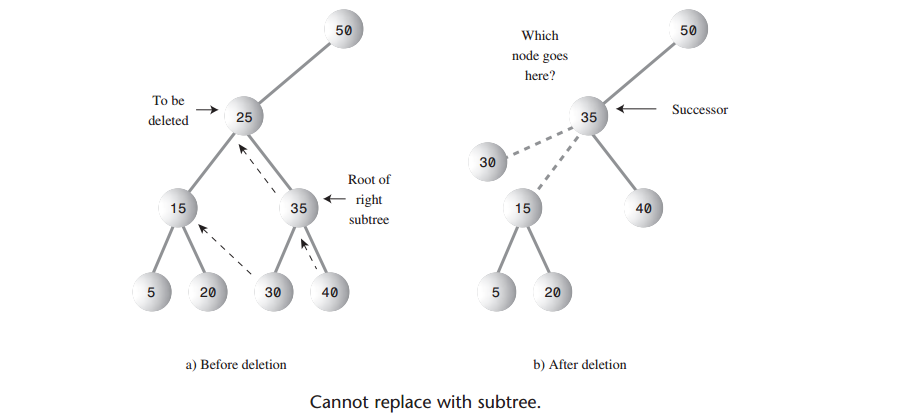
A: 窍门是:删除有两个子结点的结点,用它的中序后继来代替被删除的结点。对每一个结点来说,比该结点的关键字值大的结点就是它的中序后继。 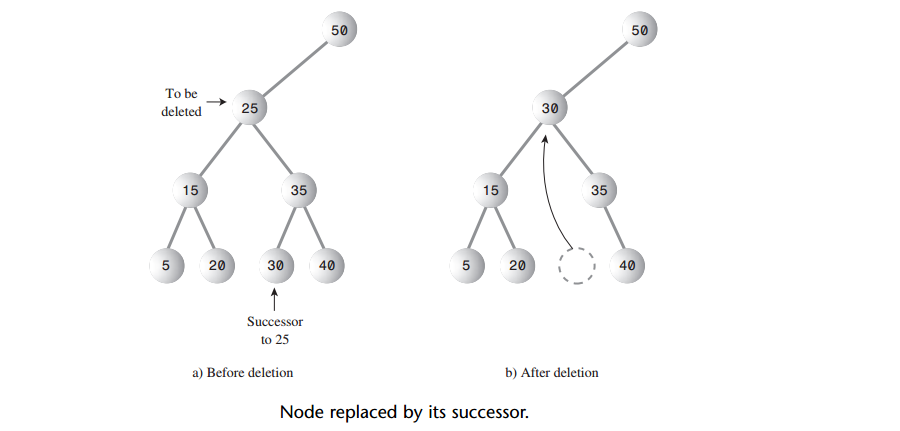
A: 假设获取中序后继结点的接口定义为Node getInorderSuccessor(Node delNode),我们先暂时不关心其具体实现,找到中序后继结点后,该结点可能与current有两种位置关系:
1) 后继结点是current的右子结点
2) 后继结点是current的右子结点的左子孙结点
Q: 后继结点是current的右子结点?
A: 只需要把后继为根的子树移动到删除的结点位置上。这个过程需要两步:
1) 把current的父结点的对应指针指向successor
2) 把successor的leftChild指针指向current的左子节点 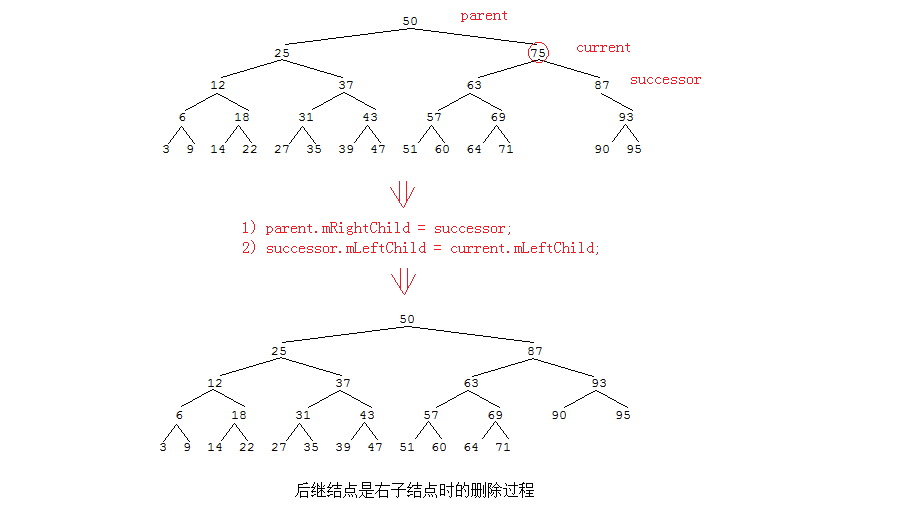
下面的代码是前面代码的延续:
// delete() continued
} else {
Node successor = getInorderSuccessor(current);
// connect parent of current to successor instead
if (current == mRoot) {
mRoot = successor;
} else if (isLeftChild) {
parent.mLeftChild = successor;
} else {
parent.mRightChild = successor;
}
// connect successor to current's left child
successor.mLeftChild = current.mLeftChild;
}
Q: 后继结点是current的右子结点的左子孙结点?
A: 执行删除操作需要以下4个步骤:
1) 把successor父结点的leftChild指针指向successor的右子结点
2) 把successor的rightChild指针指向要删除结点的右子结点
3) 把current的父结点的对应指针指向successor
4) 把successor的leftChild指针指向current的左子节点
我们发现第3、4步与后继结点是current的右子结点的代码一样,这就可以放在delete()最后的if条件句中。 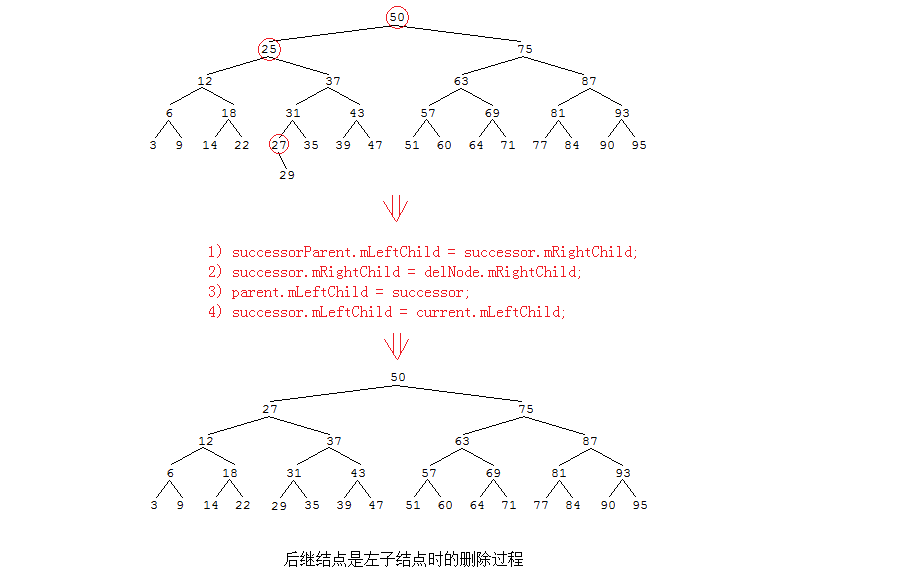
Q: 如何获取current的中序后继结点?
A: 这里实际上是要找比current关键值大的结点集合中最小的一个结点。当找到current的右子结点时,这个以右子结点为根的子树的所有结点都比current的关键字大,现在要找这棵树中最小值的结点,本篇已经介绍了如何找一棵树的最小值问题,就是顺着所有左子节点的路径找下去,因此这部分的代码实现相当地简单了。
private Node getInorderSuccessor(Node delNode) {
Node current = delNode.mRightChild; // go to right child
Node successor = null;
while (current != null) { // util no more left childrent
successor = current;
current = current.mLeftChild;
}
if (successor != delNode.mRightChild) { // if successor not right child, make connections
...
}
return successor;
}
Q: 删除是必要的吗?
A: 实际上,我们看到删除操作的处理是相当复杂的,正因为如此,一些程序可能直接在Node类加了一个标记位isDeleted,如果一个结点被删除了,就把这个结点上的这个标记位置为true。这样类似find()操作在用这个结点之前先对标记位进行判断。这样的存储中还保留着这种“已经删除”的结点。
A: 如果树中没有那么多的删除操作,这种取巧的方法也不失为一个好方法。例如,已经离职的员工的档案要永久保存在员工的记录中。
二叉树的效率
二叉树的效率与二叉树的性质密不可分。所以先了解二叉树的一些性质。
Q: 二叉树的性质?
A: 性质1 若规定根结点的层次为1,则一棵非空二叉树的第i层上最多有2i-1个结点。
A: 性质2 若规定空树的深度为0,则深度为k的二叉树的最大结点数是2k - 1
由性质1推算出,对于k层的二叉树,总共的结点数为20 + 21 + ... + 2k-1, 由等比数列的求和公式,该结果为2k - 1。
如下图,一棵满树的最大结点数与层数的关系: 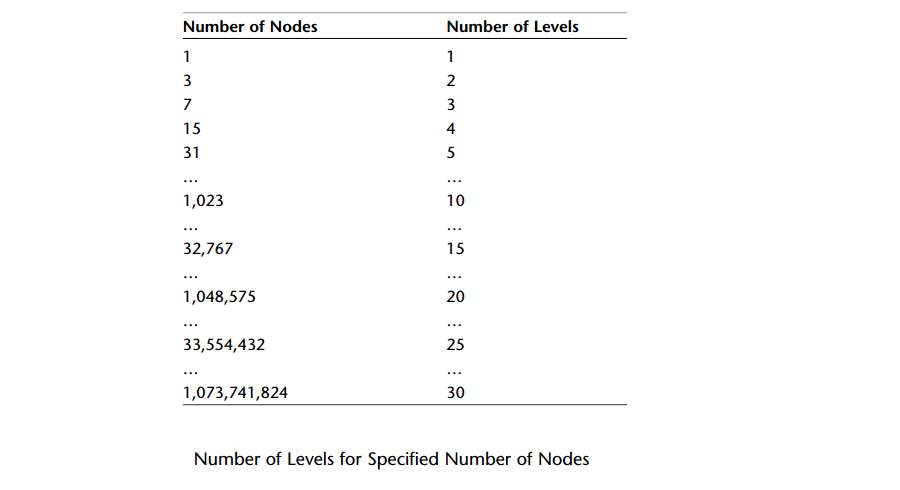
A: 性质3 具有n个结点的完全二叉树的深度k为「log2(n+1)」,其中「」表示取整,例如「3.5」等于4。
Q: 二叉树的效率?
A: 树的大部分操作都需要从上到下一层一层地查找某个结点,所以只要知道有多少层就可以知道这些操作需要多久时间。因此由性质3得出常见的树的操作时间复杂度大致是O(log2N)。
A: 如果树不满,平均查找的时间比满树的要短。
A: 在1000000个数据项的无序数组或链表中,查找数据项平均会比较500000次,但在1000000个结点的树中,只需要20(或更少)次的比较。
A: 有序数组虽然可以很快地找到数据项,但是插入数据项平均需要移动500000个数据项。而在1000000个结点的树中插入数据项只需要20次或更少的比较,在加上很短时间来连接数据项。
A: 同理,1000000个数据项的数组删除一个数据项需要平均移动500000个数据项。而在1000000个结点的树中删除只需要20次或更少的比较来找到它,在加上一点比较的时间来找它的后继,一点时间来断开这个结点的连接,以及连接它的后继结点。
A: 遍历不如其他操作快,但是遍历在大型数据库中不是常用的操作,它更常用于程序中的辅助方法来解析算术或其他的表达式,而且表达式一般不会很长。
A: 因此总体来说,树对所有常用的数据存储操作都有很高的效率。
二叉树的顺序存储结构
Q: 如何用数组表示树?
A: 结点在数组中的位置对应于它在树中的位置。下标为0的结点是根,下标为1的结点是根的左子节点,依次类推,按从左到右的顺序存储树的每一层。如下图:
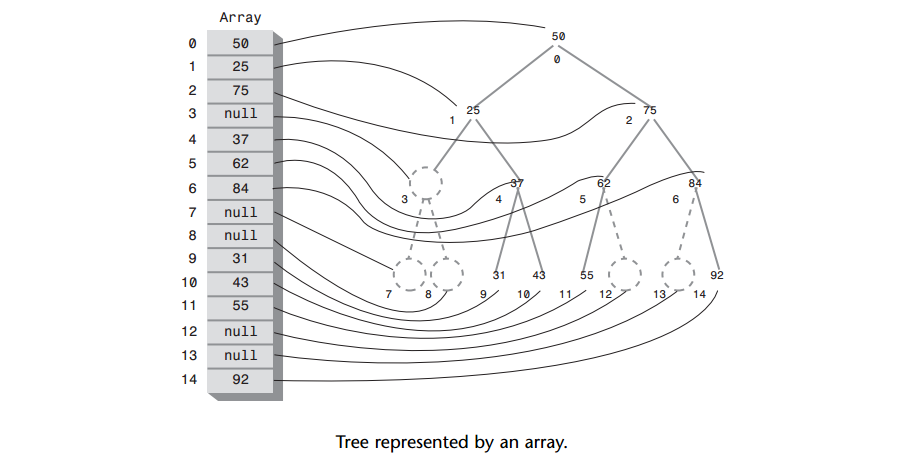
A: 树中没有结点的位置在数组中的对应位置上用0或null表示。
A: 找结点的子节点或父节点可以利用简单的算术来计算它们在数组中的索引值。
设结点索引值为index,则:
1) 它的左子节点的索引值为2 * index + 1
2) 它的右子节点的索引值为2 * index + 2
3) 它的父节点的索引值为(index-1) / 2,其中“/”符号表示整除运算
A: 大多数情况下用数组表示树不是很有效率。不满的结点和删除掉的结点在数组中留下了洞,浪费存储空间。更坏的是,删除结点时有需要移动子树的话,那么子树的每个节点都要移动到数组的新位置上,这在比较大的树中是比较费时的。
完整的Tree.java代码
示例: Tree.java
哈夫曼编码(The Huffman Code)
Q: 哈夫曼树的基本概念?
A: 路径长度:从A节点到B节点所经过的分支个数就叫做A节点到B节点的路径长度
A: 二叉树的路径长度:从二叉树的根节点到二叉树中所有叶节点的路径长度之和
A: 二叉树的带权路径长度(WPL):设二叉树有n个带权值得叶节点,定义从二叉树的根节点到二叉树中所有叶节点的路径长度与对应叶节点权值的乘积之和。即 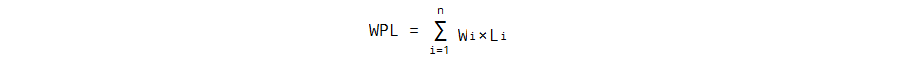
其中,Wi 为第i个叶节点的权值,Li为根节点到第i个叶节点的路径长度。
A: 给定一组具有确定权值的叶节点,可以构造出多个具有不同带权路径长度的二叉树。例如给定4个叶节点,其权值分别为1,3,5,7。可以构造出形状不同的4棵二叉树如下图所示: 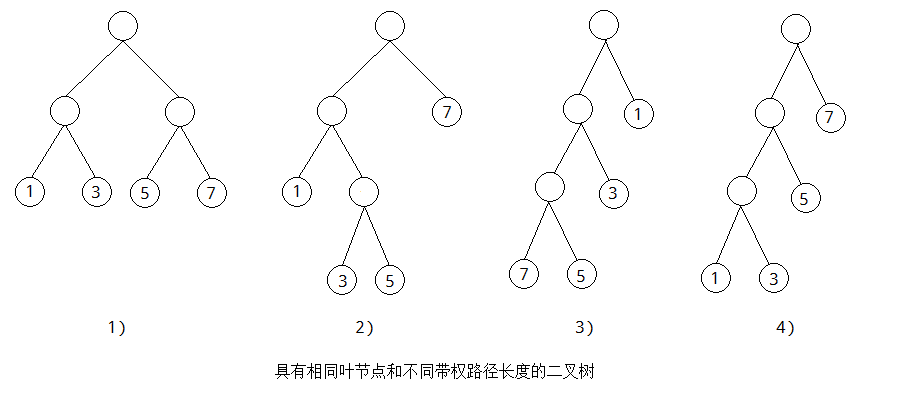
这4棵二叉树的WPL分别为:
1) WPL为1 × 2 + 3 × 2 + 5 × 2 + 7 × 2 = 32
2) WPL为1 × 2 + 3 × 3 + 5 × 3 + 7 × 1 = 33
3) WPL为1 × 1 + 3 × 2 + 5 × 3 + 7 × 3 = 43
4) WPL为1 × 3 + 3 × 3 + 5 × 2 + 7 × 1 = 29
A: 由此可见,对于一组具有确定权值的叶节点可以构造出多个具有不同带权路径长度的二叉树,其中具有最小带权路径长度的二叉树被称作哈夫曼(Huffman)树,或称最优二叉树。上图4)是一棵哈夫曼树。
A: 根据哈夫曼树的定义,一棵二叉树要使其带权路径长度WPL值最小,必须使权值越大的叶节点靠近根结点。
Q: 压缩字符?
A: ASCII码里每个字符在没有压缩的情况下占一个字符,因此每个字符都需要相同的位数(8个位),如下图: 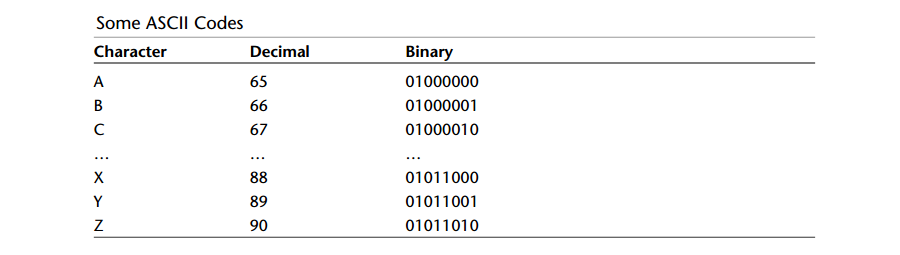
A: 最常用的压缩方法是减少最常用字符的位数量。如英文中E是最常用的字母,所以用尽可能少的位为E进行编码是非常合理的。反之Z很少用到,可以用多一点位来表示。假设压缩E用01表示,而ASCII码的z(01011010)还是使用本身ASCII值,这个时候解码就搞不清楚01011010起始的01是表示E还是表示z的开始部分,因此在编码序列时,每个代码都不能是其他代码的前缀。
A: 哈夫曼树可用于构造代码总长度最短的编码方案,具体构造方法如下:
1) 设需要编码的字符集合为{d1, d2, ..., dn}, 各个字符出现的次数集合{w1, w2, ..., wn};
2) 以d1, d2, ..., dn作为叶节点,以w1, w2, ..., wn作为各叶节点的权值构造一棵二叉树;
3) 规定哈夫曼树的左分支为0,右分支为1,则从根结点到每个节点所经过的分支对应的0和1组成的序列,就是该结点对应字符的编码;
4) 这样的代码总长度最短的不等长编码称为哈夫曼编码
A: 在哈夫曼树中,由于每个字符结点都是叶节点,而叶节点是不可能在根结点到其他叶节点的路径上,所以任何一个字符的哈夫曼编码不可能是另一个字符的哈夫曼编码的前缀。
Q: 如何创建哈夫曼树?
A: 假设要发送的消息:SUSIE SAYS IT IS EASY。下面表格列出每个字符出现的次数。 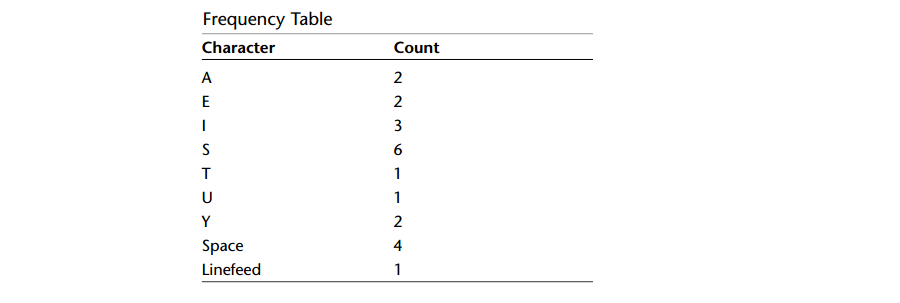
A: 下面是建立哈夫曼树的算法:
1) 一个节点包括两个数据项:字符和出现的频率
2) 为这些节点创建Tree对象,这些节点就是树的根
3) 把这些树都插入到一个优先级队列中,它们按频率排序,频率最小的节点有最高优先级
4) 从优先级队列中删除两棵树,并把它们作为一个新节点的子节点。新节点的频率是子节点频率之和,新节点字符可以是空的
5) 把这个新节点树插回优先级队列里
6) 反复重复第4)和第5)步,树会越变越大,队列中的数据项会越来越少 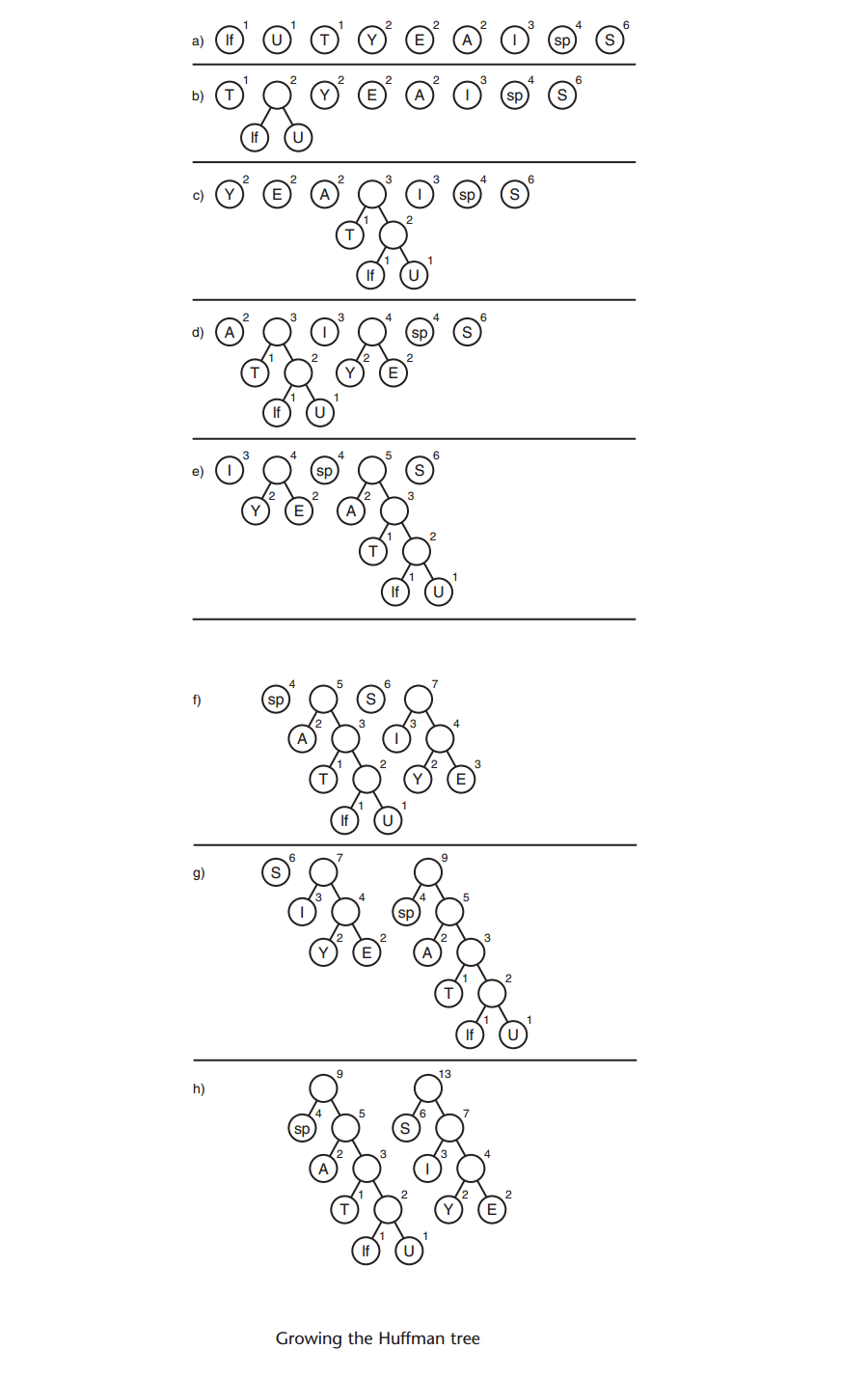
7) 当队列中只有一颗树时,它就是所建的哈夫曼树 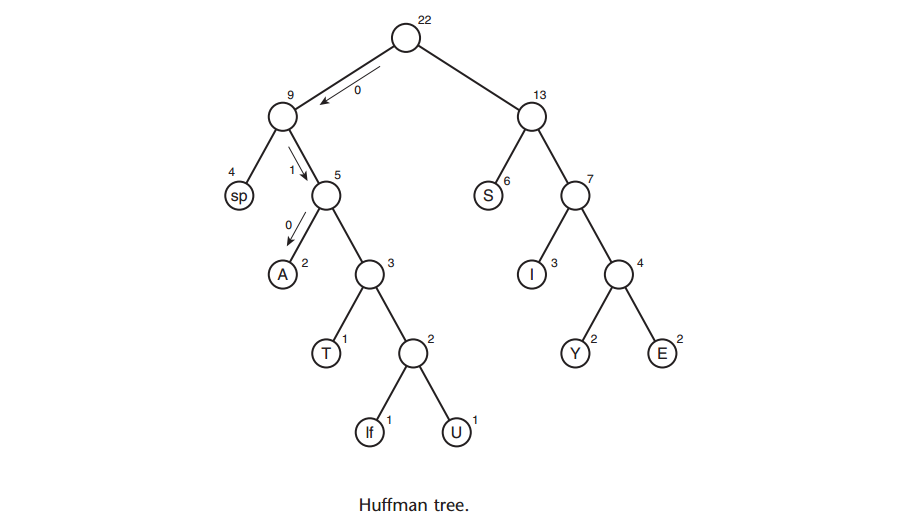
A: 对上面的哈夫曼树进行解码,那么每个字符对应的代码如下: 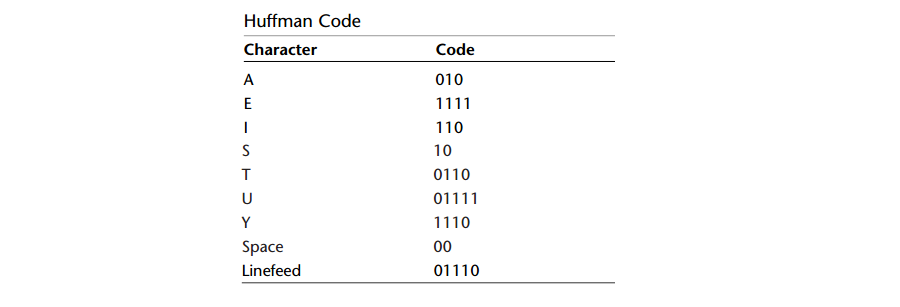
因此整个消息SUSIE SAYS IT IS EASY编码(为了清楚,这里把每个字符的代码分开显示。实际上所有位会连在一起)如下:
10 01111 10 110 1111 00 10 010 1110 10 00 110 0110 00 110 10 00 1111 010 10 1110 01110
A: 示例:Huffman.java
小结
- 树是由边(直线)连接的结点(圆)组成
- 根是树中最顶端的结点: 它没有父节点
- 二叉树中,结点最多有两个子节点
- 二叉搜索树中,所有A结点左边子孙节点的关键字值都比A小,所有右边子孙节点的关键字值都大于或等于A
- 树执行查找、插入、删除的时间复杂度都是O(logN)
- 结点表示保存在树中的数据对象
- 程序中通常用节点到子节点的引用来表示边
- 遍历树是按某种顺序来访问树中所有的结点
- 最简单的遍历方法是前序、中序和后序
- 查找结点需要比较要找的关键字值和结点的关键字值,如果要找结点关键值小就转向那个结点的左子节点,如果大就转向右子结点
- 插入需要找到要插入新节点的位置并改变它父节点的对应指针来指向它
- 中序遍历按照关键字的升序访问节点
- 前序和后序遍历对解析代数表达式是有用的
- 如果一个结点没有子节点,删除它只要把它的父结点的对应指针置为null即可
- 如果一个结点有一个子节点,把它父节点对应的指针指向它的子节点即可
- 如果一个结点有两个子节点,删除它要用它的中序后继来代替它
- A结点的中序后继是以A的右子结点为根的子树中关键值最小的那个结点
- 删除操作中,如果节点有两个子节点,会根据中序后继是被删除结点的右子结点还是被删除结点右子结点的左子孙节点出现两种不同情况
- 在计算机存储时可以用数组表示树,不过基于引用的方法更常用
- 哈夫曼树是二叉树,但不是二叉搜索树,用于数据压缩算法(哈夫曼编码)
- 哈夫曼编码中,最经常出现的字符的编码位数最少,很少出现的字符编码位数要多一些
参考
1.《Java数据结构和算法》Robert Lafore 著,第8章 - 二叉树
- 还没有人评论,欢迎说说您的想法!




 客服
客服


