题目描述:
给定一个字符串,请你找出其中不含有重复字符的 最长子串 的长度。
示例 1:
输入: "abcabcbb"
输出: 3
解释: 因为无重复字符的最长子串是
"abc",所以其长度为 3。
示例 2:
输入: "bbbbb"
输出: 1
解释: 因为无重复字符的最长子串是
"b",所以其长度为 1。
示例 3:
输入: "pwwkew"
输出: 3
解释: 因为无重复字符的最长子串是 "wke",所以其长度为 3。
请注意,你的答案必须是 子串 的长度,"pwke" 是一个子序列,不是子串。子串:串中任意个连续的字符组成的子序列称为该串的子串
方法一:暴力法
题目更新后由于时间限制,会出现 TLE(超时)。
思路
逐个检查所有的子字符串,看它是否不含有重复的字符。
关键点
假设我们有一个函数 boolean allUnique(String substring) ,如果子字符串中的字符都是唯一的,它会返回 true,否则会返回 false。 我们可以遍历给定字符串 s 的所有可能的子字符串并调用函数 allUnique。
如果事实证明返回值为 true,那么我们将会更新无重复字符子串的最大长度的答案。
现在让我们填补缺少的部分:
1.为了枚举给定字符串的所有子字符串,我们需要枚举它们开始和结束的索引。
2.要检查一个字符串是否有重复字符,我们可以使用集合。我们遍历字符串中的所有字符,并将它们逐个放入set中。
在放置一个字符之前,我们检查该集合是否已经包含它。如果包含,我们会返回false。循环结束后,我们返回true。

代码
class Solution {
public int lengthOfLongestSubstring(String s) {
//字符串长度
int n = s.length();
//值为最长子串的长度
int ans = 0;
for (int i = 0; i < n; i++) {
for (int j = i + 1; j <= n; j++) {
if (allUnique(s, i, j)) {
//更新ans的值,取最大
ans = Math.max(ans, j - i);
}
}
}
return ans;
}
/**
* 求最长无重复字符的最长子串
*
* @param s 字符串长度
* @param start 字符串当前开始位置
* @param end 字符串当前结束位置
* @return ture或false,决定要不要进入上面的if循环
*/
public boolean allUnique(String s, int start, int end) {
Set<Character> set = new HashSet<>();
for (int i = start; i < end; i++) {
//第i个字符在字符串中内容
Character ch = s.charAt(i);
//Set集合是否包含字符串ch
if (set.contains(ch)) {
return false;
}
//如果不包含,就往set集合里添加ch字符串
set.add(ch);
}
return true;
}
}
复杂度:
时间复杂度:O (n3)
方法二:滑动窗口
什么是滑动窗口?
其实就是一个队列,比如例题中的abcabcbb,进入这个队列(窗口)为abc 满足题目要求,当再进入a,队列变成了abca,这时候不满足要求。所以,我们要移动这个队列!
如何移动?
我们只要把队列的左边的元素移出就行了,直到满足题目要求!一直维持这样的队列,找出队列出现最长的长度时候,求出解!
当然滑动窗口的尺寸可以是固定也可以是动态的
思路
通过使用 HashSet 作为滑动窗口,我们可以用 O(1)O(1) 的时间来完成对字符是否在当前的子字符串中的检查。
回到我们的问题,我们使用HashSet将字符存储在当前窗口[i,,j)(最初=i)中。然后我们向右侧滑动索引j,如果它不在HashSet中,我们会继续滑动。直到si]已经存在于HashSet中。此时,我们找到的没有重复字符的最长子字符串将会以索引i开头。如果我们对所有的i这样做,就可以得到答案。
代码
public class Solution {
public int lengthOfLongestSubstring(String s) {
//字符串长度
int n = s.length();
Set<Character> set = new HashSet<>();
//定义ans为最长子串的长度,如果j的值没有在set出现过end++,知道出现start++,滑动窗口
int ans = 0, start = 0, end = 0;
//如果start和end<n就一直遍历,直到start和end都小于n
while (start < n && end < n) {
//判断Set集合是否包含end下标对应的字符串
if (!set.contains(s.charAt(end))){
//如果set里没有,则把j下标对应的字符串存进set集合, end执行完本句后+1
set.add(s.charAt(end++));
//因为end++,所有滑动窗口向后移动,并更新ans的值
ans = Math.max(ans, end - start);
}
else {
//移除Set集合start下标对应的字符串,start++,最后全部移除
set.remove(s.charAt(start++));
}
}
return ans;
}
}
复杂度
时间复杂度:O(2n)=O(n),在最糟糕的情况下,每个字符将被i和j访问两次。
空间复杂度:O(min(m,n)),与之前的方法相同。滑动窗口法需要O(k)的空间,其中k表示Set的大小。而Set的大小取决于字符串n的大小以及字符集/字母m的大小。
方法三:优化的滑动窗口
上述的方法最多需要执行2n个步骤。事实上,它可以被进一步优化为仅需要n个步骤。我们可以定义字符到索引的映射,而不是使用集合来判断一个字符是否存在。当我们找到重复的字符时,我们可以立即跳过该窗口。
也就是说,如果s[j]在[i,j)范围内有与j重复的字符,我们不需要逐渐增加i。我们可以直接跳过[i,j门范围内的所有元素,并将i变为j+1。
public class Solution {
public int lengthOfLongestSubstring(String s) {
int n = s.length(), ans = 0;
//创建map窗口
Map<Character, Integer> map = new HashMap<>();
//定义不重复子串的开始位置为 start,结束位置为 end
for (int end = 0, start = 0; end < n; end++) {
if (map.containsKey(s.charAt(end))) {
// 随着 end 不断遍历向后,会遇到与 [start, end] 区间内字符相同的情况,
// map.get(s.charAt(end)此时将字符作为 key 值,获取其 value 值,
// 此时 [start, end] 区间内不存在重复字符。
// 修改start值为之前重复字符位置之后的位置
// start更新时进行比较是因为map里key放的是所有遍历过的字符,而不仅仅是窗口里的字符。
// 所以现在的字符如果跟窗口外的字符(也就是以前的字符)重复了,start应该保持原样
start = Math.max(map.get(s.charAt(end)), start);
}
//比对当前无重复字段长度和储存的长度,选最大值并替换
//end-start+1是因为此时i,end索引仍处于不重复的位置,end还没有向后移动,取的[start,end]长度,+1因为索引从1开始
//无论是否更新 start,都会更新其 map 数据结构和结果 ans。
ans = Math.max(ans, end - start + 1);
// 将当前字符为key,value 值为字符位置 +1
// 加 1 表示从字符位置后一个才开始不重复,不然就把最后一个数给替换了
map.put(s.charAt(end), end + 1);
}
return ans;
}
}
复杂度
时间复杂度:O(n),索引j将会迭代n次。
空间复杂度(HashMap):O(min(m,n)),与之前的方法相同。
空间复杂度(Table):O(m),m是字符集的大小。
画解
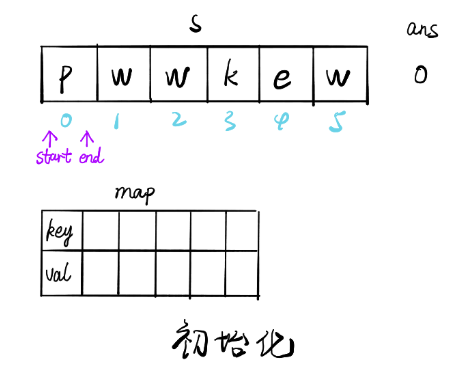
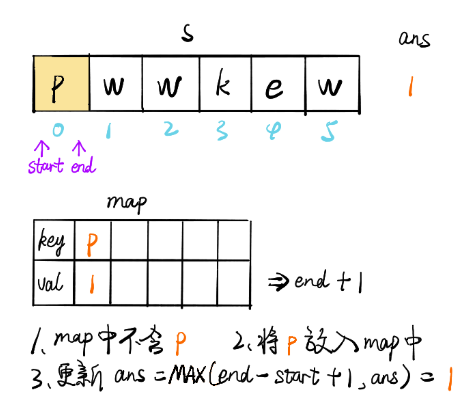
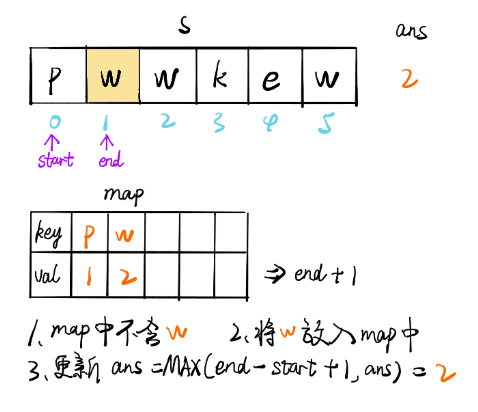
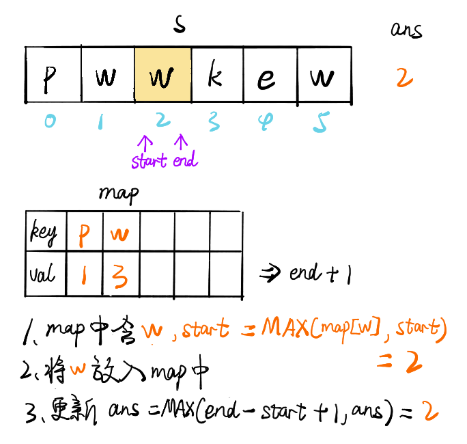
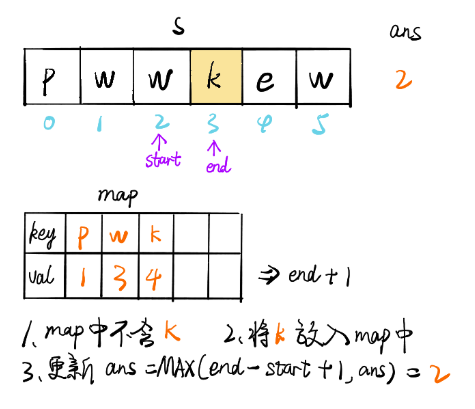
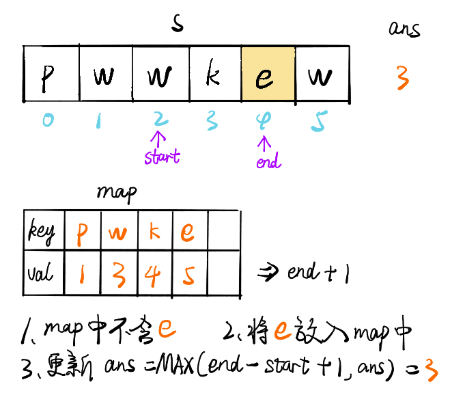
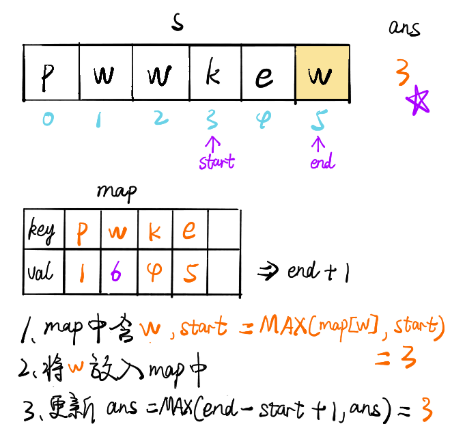
文章来源: 博客园
原文链接: https://www.cnblogs.com/xiaozhongfeixiang/p/12016590.html
- 还没有人评论,欢迎说说您的想法!




 客服
客服


