01-凸集

凸优化从入门到放弃完整教程地址：https://www.cnblogs.com/nickchen121/p/14900036.html

一、仿射集和凸集

1. 直线和线段：(x_1neq{x_2})属于空间中的两个点，则存在点 (y=theta{x_1}+(1-theta)x_2)，如果 (thetain R)，则点的集合称为直线；如果 (thetain [0,1])，则点的集合称为线段
2. 仿射集合：集合 (C) 中任意两个不同点的直线仍然在集合 (C) 中，即对于任意的 $x_1, x_2 in C $ 和 $ thetain R $，都有 (theta_1 x + (1-theta) x_2 in C)
3. 凸集：集合 (C) 中任意两个不同点的线段仍然在集合 (C) 中，即对于任意的 $x_1, x_2 in C $ 和 $ thetain [0,1] $，都有 (theta_1 x + (1-theta) x_2 in C)
   1. 图2-2，凸集：
4. 锥：对于任意 (xin C) 和 (theta geq 0) 都有 (theta x in C)，则称集合 (C) 是锥。如果 (C) 是凸的，则称为凸锥，即对于任意的 $x_1, x_2 in C $ 和 $ theta_1, theta_2 geq 0 $，都有 (theta_1 x_1 + theta_2 x_2 in C)
   4. 图 2-4，凸锥：

二、重要的例子

1. 重要的仿射集、凸集、凸锥：
   1. 空集、任意一个点、全空间 (R^n) 都是仿射的，也是凸的
   2. 直线是仿射的
   3. 通过零点的直线是仿射，也是凸锥
   4. 线段是凸的，但不仿射
   5. 一条射线是凸的，但不仿射
   6. 基点是 0 的射线是凸锥
   7. 任意子空间是仿射的、凸锥
2. 超平面：({x|a^Tx=b})，其中 (a neq 0)，可以看成法向量是 (a) 的超平面，而 (b) 决定了平面到原点的偏移
3. 半空间：({x|a^T leq b})，其中 (a neq 0)。
   1. 注：半空间是凸的，不是仿射的
   2. 图 2-7，半空间：
4. Euclid 球和椭球（凸）：
   1. Euclid 范数：(| cdot |_2)，即 (|u|_2 = {(u^T u)}^ {1/2})
   2. Euclid 球：({x|(x-x_c)^T (x-x_c) leq r^2})
   3. 椭球：({x|(x-x_c)^T P^{-1}(x-x_c) leq 1})，其中 (P^{-1}) 相当于做了空间变换，可变成斜椭球
   4. 图2-9，椭球：
5. 范数球和范数锥（凸）：
   1. 范数球：$ {x||x-x_c|leq r}$
   2. 范数锥：({ (x,t) | |x| leq t} subseteq R^{n+1})
   3. 图 2-10，(R^3) 中的二阶锥：
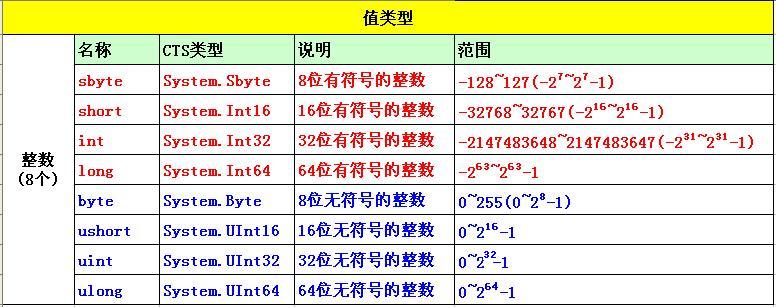
6. 多面体：有限个线性等式和不等式的解集，$ P = {x| a_j^T x leq b_j, j=1,cdots,m, c_j^T x = d_j, j = 1,cdots,p}$，通俗的讲，多面体就是有限个半空间和超平面的交集。
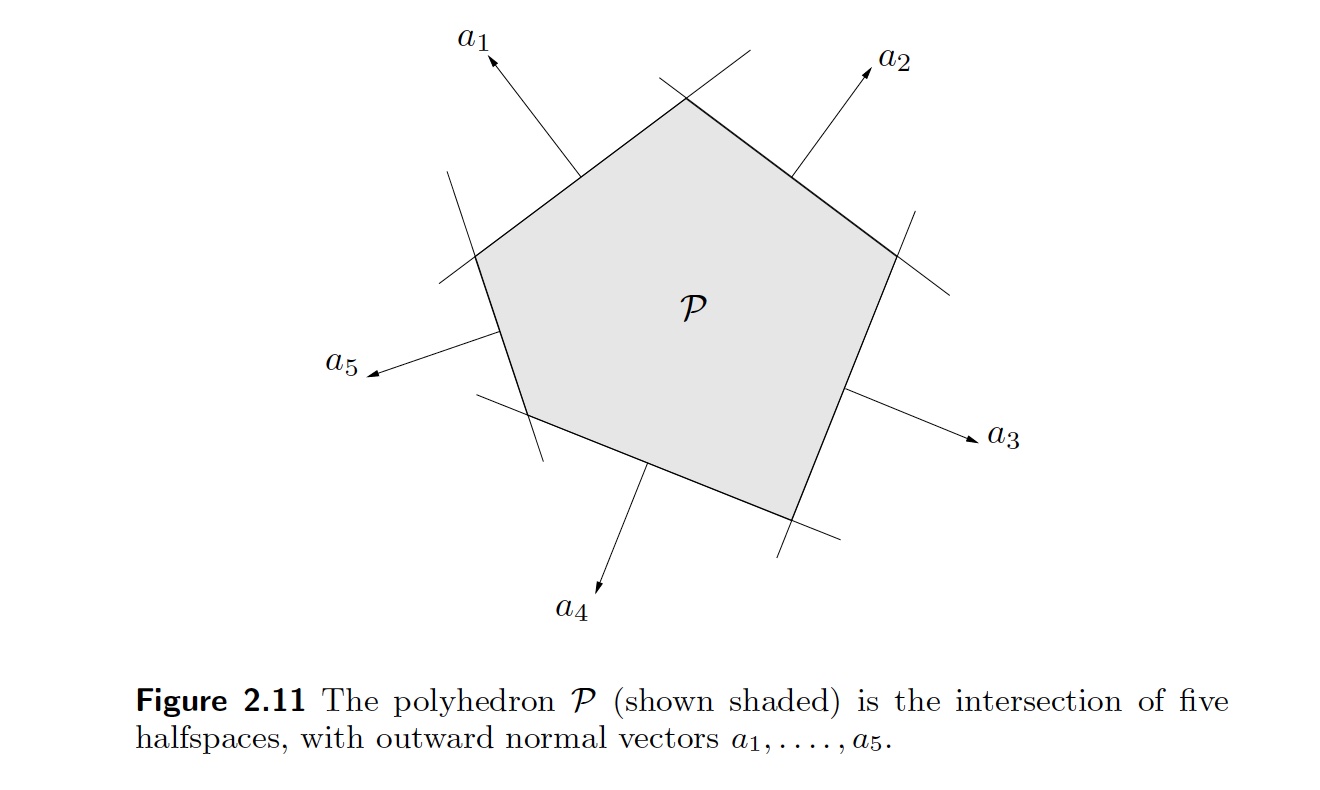
   1. 图 2-11，多面体：

三、保凸运算

四、广义不等式

五、分离与支撑超平面

六、对偶锥

• 还没有人评论，欢迎说说您的想法！

相关课程

英特尔® OpenVINO™工具套件初级课程

293015 0元 限免

基于 OpenVINO™ 的 AI 视觉应用基础课

56016 0元 限免

英特尔 OpenCV 初级认证课程

7696 0元 限免