引言：
天不生仲尼，万古如长夜。在计算机科学中，也有一个划时代的发明，B树（多路平衡查找树）及其变体（B树，b*树，b+树）；
由德国科学家（鲁道夫·拜尔 Rudolf Bayer），美国科学家（爱德华·M·麦克特 Edward Meyers McCreight）于1970年共同发明；
B树这种数据结构特别适合用于数据库与文件系统设计中，是人类精神财富的精华部分，B树不诞生，计算机在处理大数据量计算时会变得非常困难。
用途：
基本上都是软件产品最底层的，最核心的功能。
如：各种操作系统（windows，Linux，Mac）的文件系统索引，各种数据库（sqlserver、oracle、mysql、MongoDB、等等），
基本上大部分与大数据量读取有关的事务，多少都与B树家族有关，因为B树的优点太明显，特别是读取磁盘数据效率非常的高效，
查找效率O(log n)，甚至在B+树中查询速度恒定，无论多少存储多少数据，查询任何一个速度都一样。简直就是天才的发明。
诞生的原因：
在上世纪时期，计算机内存储器都非常的小，以KB为单位，比起现在动不动以G计算，简直小的可怜。
计算机运算数据时，数据是在内存中进行操作的，比如一些加减乘除、正删改查等。
举个简单的栗子：从一个数组 int a[1,2,3,4,5,6,7,8,9]中找出3，那非常简单；大概步骤如下：
1、在内存中初始化这个数组
2、获取数组指针遍历这个数组，查到3就完成
但是这个数组很大，比如包含1亿个数字怎么办？如果数组容量大大超过内存大小，那这种比较就不现实了。现在的做法都是把文件
数据存放在外存储器，比如磁盘，U盘，光盘；然后把文件分多次的拷贝数据至内存进行操作。但是读取外存储器效率对比读取内存，
差距是非常大的，一般是百万级别的差距，差6个数量级，所以这个问题不解决一切都是空谈。
好在操作系统在设计之初，就对读取外存储器进行了一定的优化，引入了“逻辑块”概念，当做操作文件的最小单元，而B树合理地利用这个“逻辑块”
功能开发的高效存储数据结构；在介绍B树特性之前，先来了解一下磁盘的基本工作原理。
磁盘简单介绍：
1）磁盘结构介绍
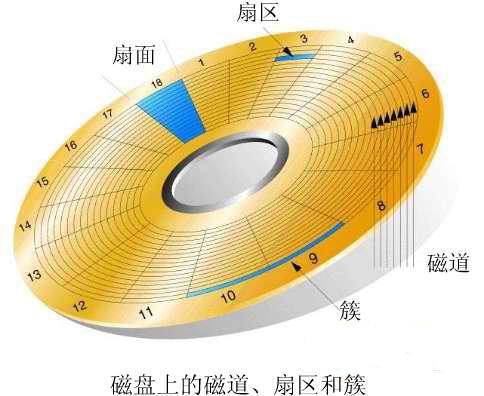
网上引用的两张图，将就看看，基本结构是：磁盘 > 盘面 > 磁道 > 扇区
左边是物理图，这个大家应该都是经常见到了，一般圆形的那部分有很多层，每一层叫盘片；右边的是示意图，代表左图的一个盘面。
每个盘面有跟多环形的磁道，每个磁道有若干段扇区组成，扇区是磁盘的最小组成单元，若干段扇区组成簇（也叫磁盘块、逻辑块等）
先看看我电脑的磁盘簇与扇区大小
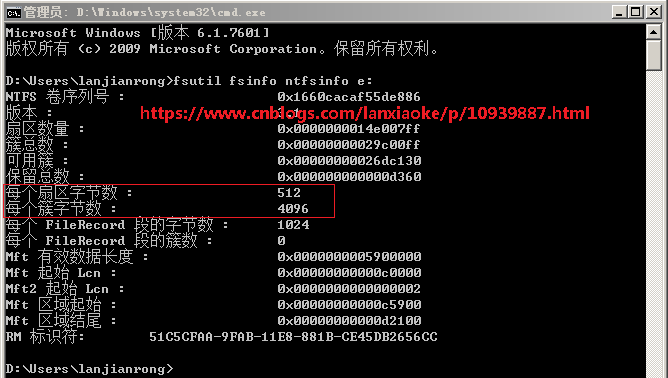
可以看到我的E盘每个扇区512个字节，每个簇4096字节，这个先记下来，后边有用到
扇区是磁盘组成的最小单元，簇是虚拟出来的，主要是为了操作系统方便读写磁盘；由于扇区比较小，数量非常多，
在寻址比较麻烦，操作系统就将相邻的几个扇区组合在一起，形成簇，再以簇为每次操作文件的最小单元。比如加载一个磁盘文件内容，
操作系统是分批次读取，每次只拷贝一个簇的单位数据，我的电脑就是一次拷贝4096字节，知道文件全部拷贝完成。
2）读写速度
磁盘读取时间是毫秒级别的一般几毫秒到十几毫秒之间，这个跟磁盘转速有点关系，还有就是数据所在磁道远近有关系；
CPU处理时间是纳秒级别，毫秒：纳秒 = 1:1000000，所以在程序设计中，读取文件是时间成本非常高的，应该尽量合理设计；
B树简介（维基百科）：
B树（英语：B-tree）是一种自平衡的树，能够保持数据有序。这种数据结构能够让查找数据、顺序访问、插入数据及删除的动作，
都在对数时间内完成。B树，概括来说是一个一般化的二叉查找树（binary search tree）一个节点可以拥有最少2个子节点。
与自平衡二叉查找树不同，B树适用于读写相对大的数据块的存储系统，例如磁盘。B树减少定位记录时所经历的中间过程，从而加快存取速度。
B树这种数据结构可以用来描述外部存储。这种数据结构常被应用在数据库和文件系统的实现上。
一个 m 阶的B树是一个有以下特性：
- 每一个节点最多有 m 个子节点
- 每一个非叶子节点（除根节点）最少有 ⌈m/2⌉ 个子节点
- 如果根节点不是叶子节点，那么它至少有两个子节点
- 有 k 个子节点的非叶子节点拥有 k − 1 个键
- 所有的叶子节点都在同一层
好吧，上边这一段看了等于没看的定义可以不看，这里有个重要的B树特性需要了解，就是B树的阶，对于阶的定义国内外是有分歧的，有的定义为度。
阶指的是节点的最大孩子数，度指的是节点的最小孩子数，我查阅了很多资料，基本上可以理解为：
1度 = 2阶，比如说3度B树，可以理解为6阶B树。这点有些疑问，有更好的说法的可以留言讨论一下。
1）内部节点：
内部节点是除叶子节点和根节点之外的所有节点。每个内部节点拥有最多 U 个，最少 L 个子节点。元素的数量总是比子节点指针的数量少1。
U 必须等于 2L 或者 2L-1。这个L一般是度数。
2）根节点：根节点拥有的子节点数量的上限和内部节点相同，但是没有下限。
3）叶子节点：叶子节点对元素的数量有相同的限制，但是没有子节点，也没有指向子节点的指针。
4）为了分析方便举例3阶3层B树
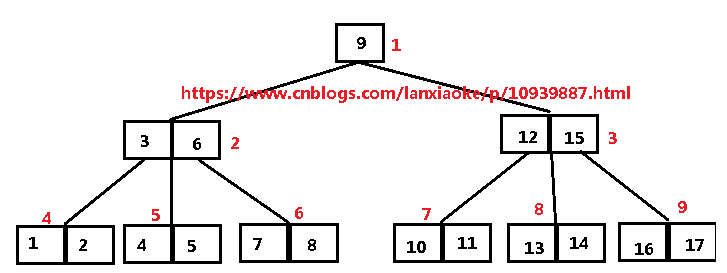
图1
从上图中可以得出以下几个信息：
- 红色数字标示整个节点（即3、6在同一个节点内，图中总共9个节点），黑色数字表示每个节点内的键值。
- 所有数据插入B树后，都是从左到右顺序排列，从根节点开始，节点左边孩子键值都小于节点键值，右边孩子键值都大于节点键值。
- 树的阶数指的是每个节点的最大孩子节点数，图中最多孩子节点数为3，即阶数=3，键值数量最少为：1，最大为：阶数 -1
数据检索分析：
依据上图分析，因为整棵树已经在内存中，相当于一个变量，数据检索首先是从根节点开始；
1）如果要查询9，首先从根节点比较，那比较一次就得到结果，
2）如果要查询第二层的3、4，首先判断根节点键值，没有匹配到，但是可以判断要检索的键值比根节点小，
所以接下来是从左孩子树继续检索，12、15也是类似，总共需要2次比较就得到结果
3）如果查询叶子节点键值，类似2），只需要3次比较就能得到结果。
4）对比普通的数组遍历查询，B树检索的时间成本没有随数据量增加而线性增加，效率大大提高。
B树的应用分析：
前面已经提到，如果树已经在内存中，那当然好办，直接遍历就好了。如果B树仅仅如此，那也和数组差别不大，同样受限于内存大小；
所以，在内存中创建整棵B树是不现实的，这不是B树的正确打开方式。
前面也已经提到，操作系统加载磁盘文件的时候，如果文件超过簇大小（即4096个字节），那会分多次的读取磁盘，直到拷贝数据完成。
这里看似一个加载动作，其实这个动作包含了N次磁盘寻址，而我们已经知道，每次磁盘寻址直至拷贝数据开销是非常大的；是CPU指令耗时百万倍以上；
这种操作应该尽量少地执行，而B树这种数据结构就是为了解决磁盘读取瓶颈这个问题而产生的。
实际应用中，B树会持久化到磁盘，然后只在内存保留一个根节点的指针。已上图1为例：
每个节点大小刚好等于簇大小，这样只需一次磁盘IO就可以获取到一整个节点的所有键值，及其所有子树的指针。
比如，查询键值8：
1）第一步，读取根节点得到键值9，以及2个子树指针，分别指向左右孩子节点，因为9 > 8，所以下一步加载左孩子节点
2）第二部，加载节点2，得到键值3、6，以及3个子树指针，因为3、6 < 8，所以下一步要加载节点2的右孩子节点
3）第三部，加载节点6，得到键值7、8，因为是叶子节点所以没有子树指针，遍历键值匹配到8，返回。
总结：
在这个3阶3层的B树中，无论查找哪一个键值，最多只需要3次磁盘操作，就算平均每次耗时10毫秒，总共需要耗时30毫秒（CPU运算耗时可以忽略）；
以此类推，3阶4层的B树，需要读取4次磁盘，耗时40毫秒，5层50毫秒，6层60毫秒，7层，8层，，，，
这样一看貌似也没什么，几十毫秒已经不能说快了，但是别忘了我们这颗树只有3阶，即一个节点保存2个键值。一个簇最多能有4096/4=1024个键值；
如果创建一个1024阶的B树，分别控制在3、4、5层的话，根据B树高度公式：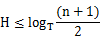
，H为层数，T为1024，n为数据总数
耗时如下：
3阶3层：能容纳2147483648（20亿）个键值，检索耗时也将30毫秒内
3阶4层：能容纳2147483648（20亿） ~ 2199023255552（2兆亿）个键值，检索耗时也将40毫秒内，当然这已经超出键值表达范围了
3阶5层：不可思议。。。
当然实际运用当中达不到1024阶，因为树持久化到磁盘时，索引结构体一般都是超过4个字节，比如12个字节，那一个簇最多能有4096/12=341个键值。
如果阶数按341来算：
3阶3层：能容纳79303642（7千万）个键值，检索耗时也将30毫秒内
3阶4层：能容纳79303642（7千万） ~ 27042541922（200亿）个键值，检索耗时也将40毫秒内
也是非常多了。。
B树简单示例：
1）首先，我们把B树基本信息定义出来
1 public class Consts 2 { 3 public const int M = 3; // B树的最小度数 4 public const int KeyMax = 2 * M - 1; // 节点包含关键字的最大个数 5 public const int KeyMin = M - 1; // 非根节点包含关键字的最小个数 6 public const int ChildMax = KeyMax + 1; // 孩子节点的最大个数 7 public const int ChildMin = KeyMin + 1; // 孩子节点的最小个数 8 }
先写个简单的demo，因为最小度数为3，那就是6阶。先实现几个简单的方法，新增，拆分，其余的合并，删除比较复杂以后有机会再看看
2）定义BTreeNode，B树节点
1 public class BTreeNode 2 { 3 private bool leaf; 4 public int[] keys; 5 public int keyNumber; 6 public BTreeNode[] children; 7 public int blockIndex; 8 public int dataIndex; 9 10 public BTreeNode(bool leaf) 11 { 12 this.leaf = leaf; 13 keys = new int[Consts.KeyMax]; 14 children = new BTreeNode[Consts.ChildMax]; 15 } 16 17 /// <summary>在未满的节点中插入键值</summary> 18 /// <param name="key">键值</param> 19 public void InsertNonFull(int key) 20 { 21 var index = keyNumber - 1; 22 23 if (leaf == true) 24 { 25 // 找到合适位置,并且移动节点键值腾出位置 26 while (index >= 0 && keys[index] > key) 27 { 28 keys[index + 1] = keys[index]; 29 index--; 30 } 31 32 // 在index后边新增键值 33 keys[index + 1] = key; 34 keyNumber = keyNumber + 1; 35 } 36 else 37 { 38 // 找到合适的子孩子索引 39 while (index >= 0 && keys[index] > key) index--; 40 41 // 如果孩子节点已满 42 if (children[index + 1].keyNumber == Consts.KeyMax) 43 { 44 // 分裂该孩子节点 45 SplitChild(index + 1, children[index + 1]); 46 47 // 分裂后中间节点上跳父节点 48 // 孩子节点已经分裂成2个节点,找到合适的一个 49 if (keys[index + 1] < key) index++; 50 } 51 52 // 插入键值 53 children[index + 1].InsertNonFull(key); 54 } 55 } 56 57 /// <summary>分裂节点</summary> 58 /// <param name="childIndex">孩子节点索引</param> 59 /// <param name="waitSplitNode">待分裂节点</param> 60 public void SplitChild(int childIndex, BTreeNode waitSplitNode) 61 { 62 var newNode = new BTreeNode(waitSplitNode.leaf); 63 newNode.keyNumber = Consts.KeyMin; 64 65 // 把待分裂的节点中的一般节点搬到新节点 66 for (var j = 0; j < Consts.KeyMin; j++) 67 { 68 newNode.keys[j] = waitSplitNode.keys[j + Consts.ChildMin]; 69 70 // 清0 71 waitSplitNode.keys[j + Consts.ChildMin] = 0; 72 } 73 74 // 如果待分裂节点不是也只节点 75 if (waitSplitNode.leaf == false) 76 { 77 for (var j = 0; j < Consts.ChildMin; j++) 78 { 79 // 把孩子节点也搬过去 80 newNode.children[j] = waitSplitNode.children[j + Consts.ChildMin]; 81 82 // 清0 83 waitSplitNode.children[j + Consts.ChildMin] = null; 84 } 85 } 86 87 waitSplitNode.keyNumber = Consts.KeyMin; 88 89 // 拷贝一般键值到新节点 90 for (var j = keyNumber; j >= childIndex + 1; j--) 91 children[j + 1] = children[j]; 92 93 children[childIndex + 1] = newNode; 94 for (var j = keyNumber - 1; j >= childIndex; j--) 95 keys[j + 1] = keys[j]; 96 97 // 把中间键值上跳至父节点 98 keys[childIndex] = waitSplitNode.keys[Consts.KeyMin]; 99 100 // 清0 101 waitSplitNode.keys[Consts.KeyMin] = 0; 102 103 // 根节点键值数自加 104 keyNumber = keyNumber + 1; 105 } 106 107 /// <summary>根据节点索引顺序打印节点键值</summary> 108 public void PrintByIndex() 109 { 110 int index; 111 for (index = 0; index < keyNumber; index++) 112 { 113 // 如果不是叶子节点, 先打印叶子子节点. 114 if (leaf == false) children[index].PrintByIndex(); 115 116 Console.Write("{0} ", keys[index]); 117 } 118 119 // 打印孩子节点 120 if (leaf == false) children[index].PrintByIndex(); 121 } 122 123 /// <summary>查找某键值是否已经存在树中</summary> 124 /// <param name="key">键值</param> 125 /// <returns></returns> 126 public BTreeNode Find(int key) 127 { 128 int index = 0; 129 while (index < keyNumber && key > keys[index]) index++; 130 131 // 该key已经存在, 返回该索引位置节点 132 if (keys[index] == key) return this; 133 134 // key 不存在,并且节点是叶子节点 135 if (leaf == true) return null; 136 137 // 递归在孩子节点中查找 138 return children[index].Find(key); 139 } 140 }
3）B树模型
1 public class BTree 2 { 3 public BTreeNode Root { get; private set; } 4 5 public BTree() { } 6 7 /// <summary>根据节点索引顺序打印节点键值</summary> 8 public void PrintByIndex() 9 { 10 if (Root == null) 11 { 12 Console.WriteLine("空树"); 13 return; 14 } 15 16 Root.PrintByIndex(); 17 } 18 19 /// <summary>查找某键值是否已经存在树中</summary> 20 /// <param name="key">键值</param> 21 /// <returns></returns> 22 public BTreeNode Find(int key) 23 { 24 if (Root == null) return null; 25 26 return Root.Find(key); 27 } 28 29 /// <summary>新增B树节点键值</summary> 30 /// <param name="key">键值</param> 31 public void Insert(int key) 32 { 33 if (Root == null) 34 { 35 Root = new BTreeNode(true); 36 Root.keys[0] = key; 37 Root.keyNumber = 1; 38 return; 39 } 40 41 if (Root.keyNumber == Consts.KeyMax) 42 { 43 var newNode = new BTreeNode(false); 44 45 newNode.children[0] = Root; 46 newNode.SplitChild(0, Root); 47 48 var index = 0; 49 if (newNode.keys[0] < key) index++; 50 51 newNode.children[index].InsertNonFull(key); 52 Root = newNode; 53 } 54 else 55 { 56 Root.InsertNonFull(key); 57 } 58 } 59 }
4）新增20个无序键值，测试一下
1 var bTree = new BTree(); 2 3 bTree.Insert(4); 4 bTree.Insert(5); 5 bTree.Insert(6); 6 bTree.Insert(1); 7 bTree.Insert(2); 8 bTree.Insert(3); 9 bTree.Insert(10); 10 bTree.Insert(11); 11 bTree.Insert(12); 12 bTree.Insert(7); 13 bTree.Insert(8); 14 bTree.Insert(9); 15 bTree.Insert(13); 16 bTree.Insert(14); 17 bTree.Insert(18); 18 bTree.Insert(19); 19 bTree.Insert(20); 20 bTree.Insert(15); 21 bTree.Insert(16); 22 bTree.Insert(17); 23 24 Console.WriteLine("输出排序后键值"); 25 bTree.PrintByIndex();
5）运行
B树持久化：
上文提到，B数不可能只存在内存而无法落地，那样没有意义。所以就需要将整棵树持久化到磁盘文件，并且还要支持快速地从磁盘文件中检索到键值；
要持久化就要考虑很多问题，像上边的简单示例是没有实际意义的，因为节点不可能只有键值与孩子树，还得有数据指针，存储位置等等，大概有以下一些问题：
- 如何保存每个节点占有字节数刚好等于一个簇大小（4096字节），因为这样就符合一次IO操作的数据交换上限？
- 如何保存每个节点的所有键值，以及这个节点下属所有子树关系？
- 如何保存每个键值对应的数据指针地址，以及指针与键值的对应关系如何维持？
- 如何保证内存与磁盘的数据交换中能够正确地还原树结构，即重建树的某部分层级与键值和子树的关系？
- 等等。。
问题比较多，非常麻烦。具体的过程就不列举了，以下展示以下修改后的B树模型。
1、先定义一个结构体
1 [StructLayout(LayoutKind.Sequential, CharSet = CharSet.Ansi, Pack = 1)] 2 public struct BlockItem 3 { 4 public int ChildBlockIndex; 5 public int Key; 6 public int DataIndex; 7 8 public BlockItem(int key, int dataIndex) 9 { 10 ChildBlockIndex = -1; 11 Key = key; 12 DataIndex = dataIndex; 13 } 14 }
结构体总共12字节，为了能够持久化整棵B树到磁盘，加入了ChildBlockIndex子孩子节点块索引,根据这个块索引在下一次重建子孩子树层级关系时就知道从
文件的那个位置开始读取；Key键值，DataIndex数据索引，数据索引也是一个文件位置记录，跟ChildBlockIndex差不多，这样检索到key后就知道从
文件哪个位置获取真正的数据。为了更形象了解B树应用，我画了一个结构体的示意图：
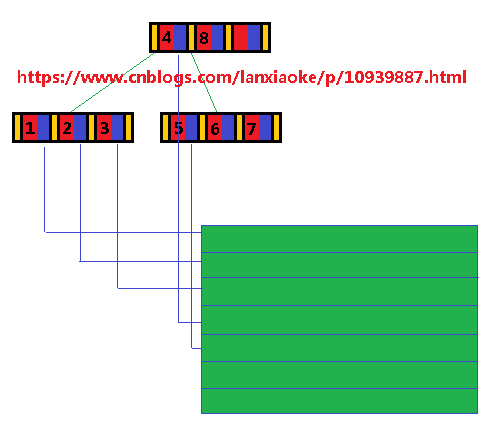
0、总共3个节点，每个节点由N个结构体组成，最末尾只有孩子指针，没有数据与键值
1、黄色为子树块索引,即ChildBlockIndex,指向这个子孩子树所有数据在文件中的位置
2、红色为键值，即Key，键值一般是唯一的，不允许重复
3、蓝色为数据块索引，即DataIndex，指向键值对应的数据在文件中的什么位置开始，然后读取一个结构体的长度即可
4、底下绿色的一块是数据指针指向的具体数据块
2、数据结构体
1 [StructLayout(LayoutKind.Sequential, CharSet = CharSet.Ansi, Pack = 1)] 2 public struct SDataTest 3 { 4 public int Idx; 5 public int Age; 6 public byte Sex; 7 8 [MarshalAs(UnmanagedType.ByValArray, SizeConst = 20)] 9 public byte[] Name; 10 11 public byte Valid; 12 };
3、B树节点类修改改一下，这个就不解释了，复习一下程序员基本功，啃代码。
1 public class BTreeNode 2 { 3 private BTree tree; 4 private bool leaf; 5 6 public int keyNumber; 7 public BlockItem[] keys; 8 public BTreeNode[] children; 9 10 public int blockIndex; 11 public int findIndex; 12 13 public BTreeNode(BTree tree, bool leaf) 14 { 15 this.tree = tree; 16 this.leaf = leaf; 17 keys = new BlockItem[Consts.KeyMax]; 18 children = new BTreeNode[Consts.ChildMax]; 19 blockIndex = Consts.BlockIndex++; 20 } 21 22 /// <summary>在未满的节点中插入键值</summary> 23 /// <param name="key">键值</param> 24 public void InsertNonFull(BlockItem item) 25 { 26 var index = keyNumber - 1; 27 28 if (leaf == true) 29 { 30 // 找到合适位置,并且移动节点键值腾出位置 31 while (index >= 0 && keys[index].Key > item.Key) 32 { 33 keys[index + 1] = keys[index]; 34 index--; 35 } 36 37 // 在index后边新增键值 38 keys[index + 1] = item; 39 keyNumber = keyNumber + 1; 40 } 41 else 42 { 43 // 找到合适的子孩子索引 44 while (index >= 0 && keys[index].Key > item.Key) index--; 45 46 // 如果孩子节点已满 47 if (children[index + 1].keyNumber == Consts.KeyMax) 48 { 49 // 分裂该孩子节点 50 SplitChild(index + 1, children[index + 1]); 51 52 // 分裂后中间节点上跳父节点 53 // 孩子节点已经分裂成2个节点,找到合适的一个 54 if (keys[index + 1].Key < item.Key) index++; 55 } 56 57 // 插入键值 58 children[index + 1].InsertNonFull(item); 59 } 60 } 61 62 /// <summary>分裂节点</summary> 63 /// <param name="childIndex">孩子节点索引</param> 64 /// <param name="waitSplitNode">待分裂节点</param> 65 public void SplitChild(int childIndex, BTreeNode waitSplitNode) 66 { 67 var newNode = new BTreeNode(tree, waitSplitNode.leaf); 68 newNode.keyNumber = Consts.KeyMin; 69 70 // 把待分裂的节点中的一般节点搬到新节点 71 for (var j = 0; j < Consts.KeyMin; j++) 72 { 73 newNode.keys[j] = waitSplitNode.keys[j + Consts.ChildMin]; 74 75 // 清0 76 waitSplitNode.keys[j + Consts.ChildMin] = default(BlockItem); 77 } 78 79 // 如果待分裂节点不是也只节点 80 if (waitSplitNode.leaf == false) 81 { 82 for (var j = 0; j < Consts.ChildMin; j++) 83 { 84 // 把孩子节点也搬过去 85 newNode.children[j] = waitSplitNode.children[j + Consts.ChildMin]; 86 87 // 清0 88 waitSplitNode.children[j + Consts.ChildMin] = null; 89 } 90 } 91 92 waitSplitNode.keyNumber = Consts.KeyMin; 93 94 for (var j = keyNumber; j >= childIndex + 1; j--) 95 children[j + 1] = children[j]; 96 97 children[childIndex + 1] = newNode; 98 99 for (var j = keyNumber - 1; j >= childIndex; j--) 100 keys[j + 1] = keys[j]; 101 102 // 把中间键值上跳至父节点 103 keys[childIndex] = waitSplitNode.keys[Consts.KeyMin]; 104 105 // 清0 106 waitSplitNode.keys[Consts.KeyMin] = default(BlockItem); 107 108 // 根节点键值数自加 109 keyNumber = keyNumber + 1; 110 } 111 112 /// <summary>根据节点索引顺序打印节点键值</summary> 113 public void PrintByIndex() 114 { 115 int index; 116 for (index = 0; index < keyNumber; index++) 117 { 118 // 如果不是叶子节点, 先打印叶子子节点. 119 if (leaf == false) children[index].PrintByIndex(); 120 121 Console.Write("{0} ", keys[index].Key); 122 } 123 124 // 打印孩子节点 125 if (leaf == false) children[index].PrintByIndex(); 126 } 127 128 /// <summary>查找某键值是否已经存在树中</summary> 129 /// <param name="item">键值</param> 130 /// <returns></returns> 131 public BTreeNode Find(BlockItem item) 132 { 133 findIndex = 0; 134 int index = 0; 135 while (index < keyNumber && item.Key > keys[index].Key) index++; 136 137 // 遍历全部都未找到,索引计数减1 138 if (index > 0 && index == keyNumber) index--; 139 140 // 该key已经存在, 返回该索引位置节点 141 if (keys[index].Key == item.Key) 142 { 143 findIndex = index; 144 return this; 145 } 146 147 // key 不存在,并且节点是叶子节点 148 if (leaf == true) return null; 149 150 // 重建children[index]数据结构 151 var childBlockIndex = keys[index].ChildBlockIndex; 152 tree.LoadNodeByBlock(ref children[index], childBlockIndex); 153 154 // 递归在孩子节点中查找 155 if (children[index] == null) return null; 156 return children[index].Find(item); 157 } 158 }
4、B树模型也要修改一下 ，不解释
1 public class BTree 2 { 3 private FileStream rwFS; 4 5 public BTreeNode Root; 6 7 public BTree(string fullName) 8 { 9 rwFS = new FileStream(fullName, FileMode.OpenOrCreate, FileAccess.ReadWrite); 10 11 // 创建10M的空间,用做索引存储 12 if (rwFS.Length == 0) 13 { 14 rwFS.SetLength(Consts.IndexTotalSize); 15 } 16 17 // 从数据文件重建根节点,内存只保存根节点 18 LoadNodeByBlock(ref Root, 0); 19 } 20 21 public void LoadNodeByBlock(ref BTreeNode node, int blockIndex) 22 { 23 var items = Helper.Read(rwFS,blockIndex); 24 if (items.Count > 0) 25 { 26 var isLeaf = items[0].ChildBlockIndex == Consts.NoChild; 27 28 node = new BTreeNode(this, isLeaf); 29 node.blockIndex = blockIndex; 30 node.keys = items.ToArray(); 31 node.keyNumber = items.Count; 32 } 33 } 34 35 /// <summary>根据节点索引顺序打印节点键值</summary> 36 public void PrintByIndex() 37 { 38 if (Root == null) 39 { 40 Console.WriteLine("空树"); 41 return; 42 } 43 44 Root.PrintByIndex(); 45 } 46 47 /// <summary>查找某键值是否已经存在树中</summary> 48 /// <param name="item">键值</param> 49 /// <returns></returns> 50 public BTreeNode Find(BlockItem item) 51 { 52 if (Root == null) return null; 53 54 return Root.Find(item); 55 } 56 public BTreeNode Find(int key) 57 { 58 return Find(new BlockItem() { Key = key }); 59 } 60 61 /// <summary>新增B树节点键值</summary> 62 /// <param name="item">键值</param> 63 private void Insert(BlockItem item) 64 { 65 if (Root == null) 66 { 67 Root = new BTreeNode(this, true); 68 Root.keys[0] = item; 69 Root.keyNumber = 1; 70 } 71 else 72 { 73 if (Root.keyNumber == Consts.KeyMax) 74 { 75 var newNode = new BTreeNode(this, false); 76 77 newNode.children[0] = Root; 78 newNode.SplitChild(0, Root); 79 80 var index = 0; 81 if (newNode.keys[0].Key < item.Key) index++; 82 83 newNode.children[index].InsertNonFull(item); 84 Root = newNode; 85 } 86 else 87 { 88 Root.InsertNonFull(item); 89 } 90 } 91 } 92 93 public void Insert(SDataTest data) 94 { 95 var item = new BlockItem() 96 { 97 Key = data.Idx 98 }; 99 100 var node = Find(item); 101 if (node != null) 102 { 103 Console.WriteLine("键值已经存在,info:{0}", item.Key); 104 return; 105 } 106 107 // 保存数据 108 item.DataIndex = Helper.InsertData(rwFS, data); 109 110 // 保存索引 111 if (item.DataIndex >= 0) 112 Insert(item); 113 } 114 115 /// <summary>持久化整棵树</summary> 116 public void SaveIndexAll() 117 { 118 SaveIndex(Root); 119 } 120 121 /// <summary>持久化某节点以下的树枝</summary> 122 /// <param name="node">某节点</param> 123 public void SaveIndex(BTreeNode node) 124 { 125 var bw = new BinaryWriter(rwFS); 126 var keyItem = default(BlockItem); 127 128 // 第一层 129 var nodeL1 = node; 130 if (nodeL1 == null) return; 131 132 for (var i = 0; i <= nodeL1.keyNumber; i++) 133 { 134 keyItem = default(BlockItem); 135 if (i < nodeL1.keyNumber) keyItem = nodeL1.keys[i]; 136 137 SaveIndex(bw, 0, i, nodeL1.children[i], keyItem); 138 139 // 第二层 140 var nodeL2 = nodeL1.children[i]; 141 if (nodeL2 == null) continue; 142 143 for (var j = 0; j <= nodeL2.keyNumber; j++) 144 { 145 keyItem = default(BlockItem); 146 if (j < nodeL2.keyNumber) keyItem = nodeL2.keys[j]; 147 148 SaveIndex(bw, nodeL2.blockIndex, j, nodeL2.children[j], keyItem); 149 150 // 第三层 151 var nodeL3 = nodeL2.children[j]; 152 if (nodeL3 == null) continue; 153 154 for (var k = 0; k <= nodeL3.keyNumber; k++) 155 { 156 keyItem = default(BlockItem); 157 if (k < nodeL3.keyNumber) keyItem = nodeL3.keys[k]; 158 159 SaveIndex(bw, nodeL3.blockIndex, k, nodeL3.children[k], keyItem); 160 161 // 第四层 162 var nodeL4 = nodeL3.children[k]; 163 if (nodeL4 == null) continue; 164 165 for (var l = 0; l <= nodeL4.keyNumber; l++) 166 { 167 keyItem = default(BlockItem); 168 if (l < nodeL4.keyNumber) keyItem = nodeL4.keys[l]; 169 170 SaveIndex(bw, nodeL4.blockIndex, l, nodeL4.children[l], keyItem); 171 172 // 第五层 173 var nodeL5 = nodeL4.children[l]; 174 if (nodeL5 == null) continue; 175 176 for (var z = 0; z <= nodeL5.keyNumber; z++) 177 { 178 keyItem = default(BlockItem); 179 if (z < nodeL5.keyNumber) keyItem = nodeL5.keys[z]; 180 181 SaveIndex(bw, nodeL5.blockIndex, z, nodeL5.children[z], keyItem); 182 } 183 } 184 } 185 } 186 } 187 } 188 private void SaveIndex(BinaryWriter bw, int blockIndex, int num, BTreeNode node, BlockItem item) 189 { 190 bw.Seek((blockIndex * Consts.BlockSize) + (num * Consts.IndexSize), SeekOrigin.Begin); 191 bw.Write(node == null ? Consts.NoChild : node.blockIndex); 192 bw.Write(item.Key); 193 bw.Write(item.DataIndex); 194 bw.Flush(); 195 } 196 197 public SDataTest LoadData(int dataIndex) 198 { 199 return Helper.Load(rwFS, dataIndex); 200 } 201 }
5、写测试
1 private static void InsertTest(ref BTree bTree) 2 { 3 // 新增测试数据 4 for (int i = 1; i <= Consts.TotalKeyNumber; i++) 5 { 6 bTree.Insert(new SDataTest() 7 { 8 Idx = i, 9 Age = i, 10 Sex = 1, 11 Name = Helper.Copy("Name(" + i.ToString() + ")", 20), 12 Valid = 1 13 }); 14 } 15 16 Console.WriteLine("测试数据添加完毕,共新增{0}条数据", Consts.TotalKeyNumber); 17 }
6、读测试
1 private static void FindTest(ref BTree bTree) 2 { 3 var count = 0; 4 5 // 校验数据查找 6 for (int i = 1; i <= Consts.TotalKeyNumber; i++) 7 { 8 var node = bTree.Find(i); 9 if (node == null) 10 { 11 //Console.WriteLine("未找到{0}", i); 12 continue; 13 } 14 15 //Console.WriteLine("findIndex:{0},key:{1},dataIndex:{2}", node.findIndex, node.keys[node.findIndex].Key, node.keys[node.findIndex].DataIndex); 16 17 count++; 18 if (count % 10000 == 0) 19 { 20 var data = bTree.LoadData(node.keys[node.findIndex].DataIndex); 21 var name = Encoding.Default.GetString(data.Name).TrimEnd(' '); 22 Console.WriteLine("Idx:{0},Age:{1},Sex:{2},Name:{3},Valid:{4}", data.Idx, data.Age, data.Sex, name, data.Valid); 23 } 24 } 25 26 Console.WriteLine("有效数据个数:{0}", count); 27 }
7、最后测试一下
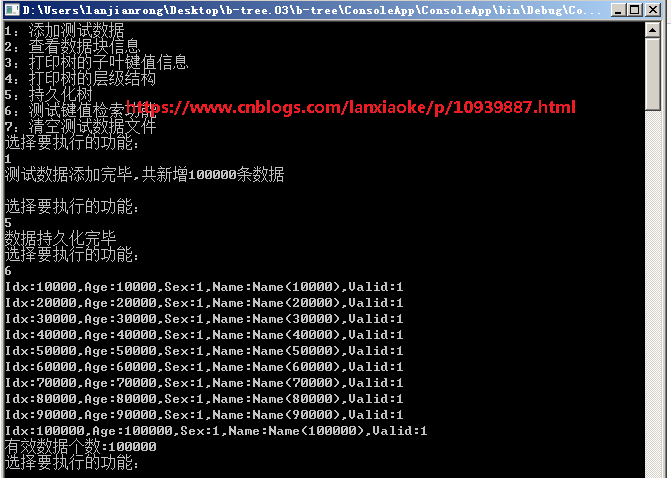
8、测试查询时间
1 private static void CheckLoadTime(ref BTree bTree, int key) 2 { 3 var start = DateTime.Now; 4 var node = bTree.Find(key); 5 if (node == null) return; 6 7 Console.WriteLine("查找{0},耗时:{1}", key.ToString(), (DateTime.Now - start).TotalMilliseconds.ToString()); 8 9 var data = bTree.LoadData(node.keys[node.findIndex].DataIndex); 10 var name = Encoding.Default.GetString(data.Name).TrimEnd(' '); 11 Console.WriteLine("Idx:{0},Age:{1},Sex:{2},Name:{3},Valid:{4}", data.Idx, data.Age, data.Sex, name, data.Valid); 12 Console.WriteLine(); 13 }
1 CheckLoadTime(ref bTree, 1000); 2 CheckLoadTime(ref bTree, 10000); 3 CheckLoadTime(ref bTree, 50000); 4 CheckLoadTime(ref bTree, 100000);
9、重新生成10000000条数据，测试查询效率
1 CheckLoadTime(ref bTree, 100000); 2 CheckLoadTime(ref bTree, 1000000); 3 CheckLoadTime(ref bTree, 3000000); 4 CheckLoadTime(ref bTree, 5000000); 5 CheckLoadTime(ref bTree, 8000000); 6 CheckLoadTime(ref bTree, 10000000);
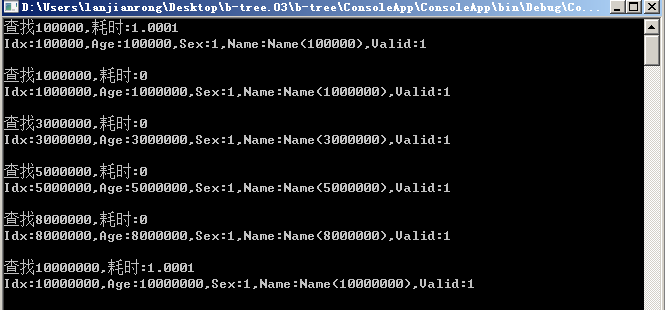
全是1毫秒内返回，数据检索效率非常高，
学习历程：
实际上最初在学校潦草学了一遍【数据结构】之后，工作那么多年都用不着这方面的知识点，早就忘得一干二净了。
重新引起我兴趣的是2017年下半年，当时一个项目需要用到共享内存作为快速读写数据的底层核心功能。在设计共享内存存储关系时，
就遇到了索引的快速检索要求，第一次是顺序检索，当数据量达到5万以上时系统就崩了，检索速度太慢；后来改为二分查找法，轻松达到20万数据；
达到20万后就差不多到了单机处理性能瓶颈了，因为CPU不够用，除了检索还需要做其他的业务计算；
那时候就一直在搜索快速查找的各种算法，什么快速排序算法、堆排序算法、归并排序、二分查找算法、DFS（深度优先搜索）、BFS(广度优先搜索)，
基本上都了解了一遍，但是看得头疼，没去实践。最后看到树结构，引起我很大兴趣，就是园友nullzx的这篇：B+树在磁盘存储中的应用，
这让我了解到原来数据库是这样读写的，这很有意思，得造个轮子自己试一次。
粗陋仓促写成，恐怕有很多地方有漏洞，所以如果文中有错误的地方，欢迎留言讨论，但是拒绝一波流的吐槽，我可是会删低级评论的。
- 还没有人评论，欢迎说说您的想法！
客服
