dfs深搜封闭岛屿+动态规划地图里的宝箱+LRU缓存类

457 0 0

作者:WELCOME TO ivanlee717！！！！

wangyi

记录一次某大厂笔试的AC过程

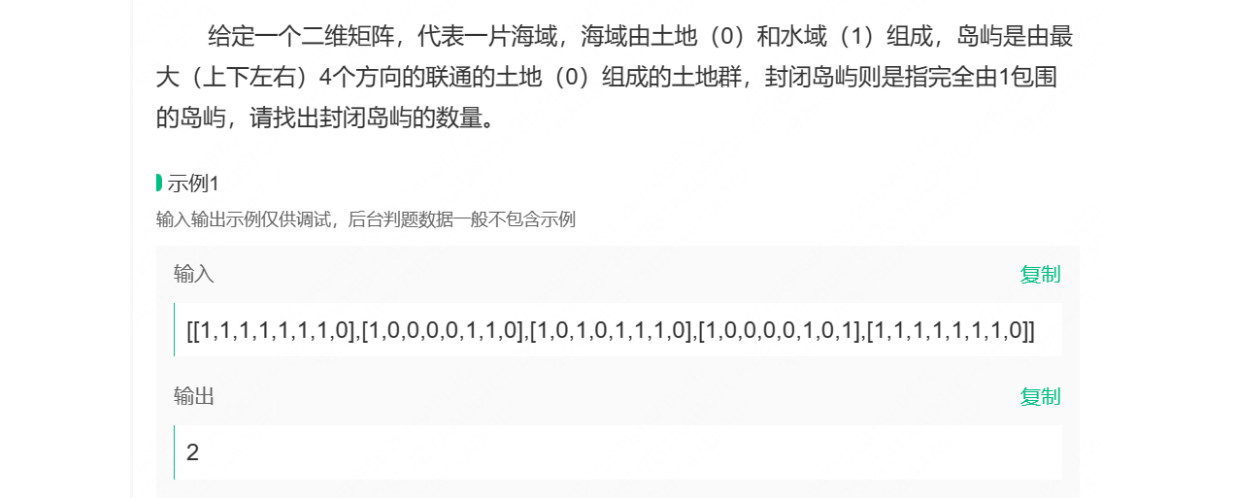
给定一个二维矩阵，代表一片海域，海域由土地(0)和水域(1)组成，岛屿是由最大(上下左右)4个方向的联通的土地(0)组成的土地群，封闭岛屿则是指完全由1包围的岛屿，请找出封闭岛屿的数量。

题中给的图可以看到外围的1已经用蓝色标出来的了，但是真正是封闭岛屿的只有这一块，

class Solution:
    def closedIsland(self , grid: List[List[int]]) -> int:
        # write code here
        if not grid or not grid[0]:
            return 0
        m, n = len(grid), len(grid[0])
        dir = [(0,1),(0,-1),(1,0),(-1,0)]
        def dfs(i,j):
            if i<0 or j<0 or i>=m or j >=n:
                return False
            if grid[i][j] == 1:
                return True

            grid[i][j] = 1

            res = [dfs(i+dx,j+dy) for dx, dy in dir]
            return all(res)

        return sum(dfs(i,j) for i in range(m) for j in range(n) if grid[i][j] == 0)

这是一个比较经典的深度搜索问题，我们可以通过遍历每个格子，当遇到土地0时进行四个方向的搜索，同时标记已经遍历过的格子，最直接的办法就是把他变成水域。使用all函数如果iterable的所有元素不为0、''、False或者iterable为空，all(iterable)返回True，否则返回False；

为了庆祝某游戏周年庆，策划组正在为该游戏设计一次福利活动，他们希望推出一个迷宫寻宝小游戏，让玩家探索迷宫中的宝箱，玩家可以在不同的宝箱中获取不同数量的金币，并最终通过金币兑换游戏中的限定道具。

为了增加玩法的多样性，策划同学希望能够提供2种寻宝地图，但是每个玩家一天只能选择一张寻宝地图进行探索。同时策划同学提供了宝箱价值的列表，但是这个宝箱价值能不能被合理投放在两个地图中尚未验证，因此希望能借助程序的手段来验证宝箱价值的设计是否合理，具体要求如下:
1.每个宝箱必须目只能被放置在一个地图中，不能重复利用。
2.为了确保玩家获得的奖励数量，策划同学提供了一个“保底值”，两张地图的宝箱奖励总和必须都大于等于这个保底值。

现在需要请你来设计投放程序，假设保底值为k，每个宝箱的价值都是正整数，并被存放干数组nums中，需要通过返回值告诉策划，这样的宝箱价值能够有几种合理的投放方式.

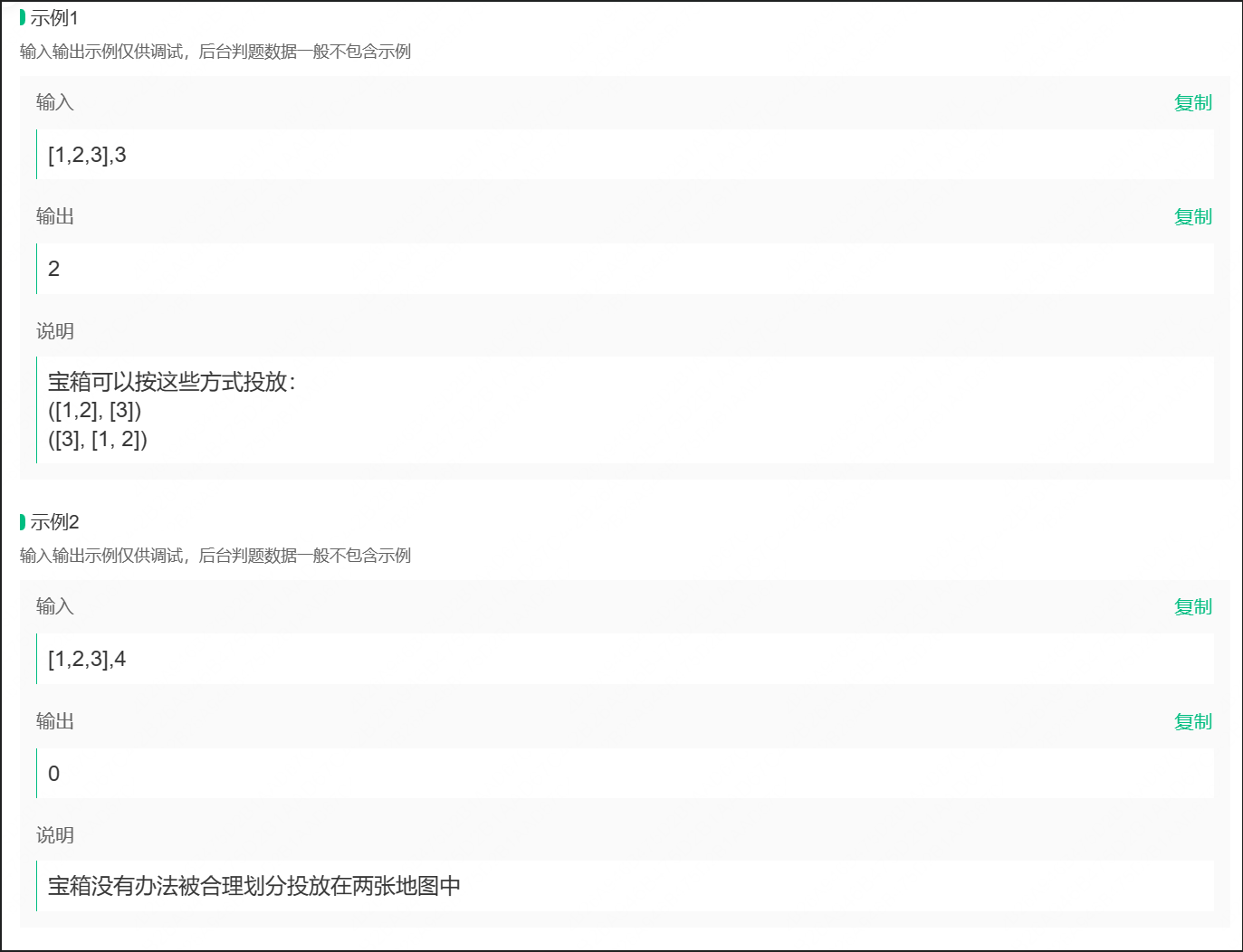
由于每个宝箱只能被选择一次，并且需要计算所有可能的宝箱组合，对于每一个宝箱，只存在两种情况，选入当前地图或者不选入当前地图。同时在计算某个价值是否能通过前i个宝箱价值的组合获取时，可能会出现重复计算，使用动态规划存储子问题的结果来提高运行效率。

动态规划过程：

定义一个dp[i]存储一个地图的宝箱总价值恰好为i的分配的方案数

状态转移：对于每一个价值为v的宝箱，我们可以选择选入或者不选入当前地图。如果选入，则有dp[i-v]种方案；如果不选入，则有dp[i]种方法，所以dp[i] = dp[i] + dp[i-v]

初始化状态：没有任何元素时，和为0的方案数为1，所以dp[0] = 1

遍历整个数组，将i>=k并且i<=total_value-k的方法进行求和

class Solution:
    def countPartitions(self, nums: List[int], k: int) -> int:
        n = len(nums)
        total_value = sum(nums)

        if total_value < 2 * k:
            return 0

        dp = [0] * (total_value + 1)
        dp[0] = 1

        for i in nums:
            for j in range(total_value, i - 1, -1):
                dp[j] += dp[j - i]

        count = sum(dp[i] for i in range(k, total_value - k + 1))
        return count

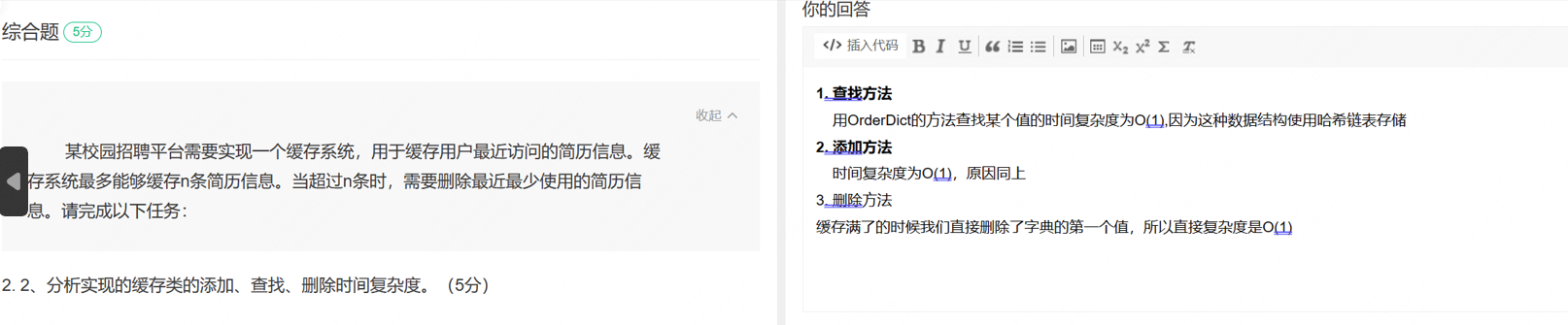
第三个设计题设计一个LRU缓存类